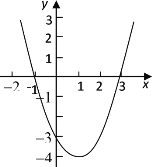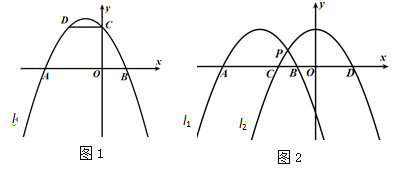题目内容
【题目】某数学兴趣小组在探究函数![]() 的图象和性质时,经历了以下探究过程:
的图象和性质时,经历了以下探究过程:
(1)列表如下:

写出表中m、n的值:m= ,n= ;
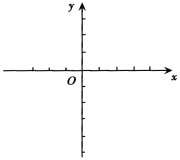
(2)描点并在图中画出函数的大致图象;
(3)根据函数图象,完成以下问题:
①观察函数![]() 的图象,以下说法正确的有 (填写正确的序号)
的图象,以下说法正确的有 (填写正确的序号)
A.对称轴是直线x=1;
B.函数![]() 的图象有两个最低点,其坐标分别是(﹣1,2)、(1,2);
的图象有两个最低点,其坐标分别是(﹣1,2)、(1,2);
C.当﹣1<x<1时,y随x的增大而增大;
D.当函数![]() 的图象向下平移3个单位时,图象与x轴有三个公共点;
的图象向下平移3个单位时,图象与x轴有三个公共点;
E.函数![]() 的图象,可以看作是函数
的图象,可以看作是函数![]() 的图象向右平移2个单位得到.
的图象向右平移2个单位得到.
②结合图象探究发现,当m满足 时,方程![]() 有四个解.
有四个解.
③设函数![]() 的图象与其对称轴相交于P点,当直线y=n和函数
的图象与其对称轴相交于P点,当直线y=n和函数![]() 图象只有两个交点时,且这两个交点与点P所构成的三角形是等腰直角三角形,则n的值为____________.
图象只有两个交点时,且这两个交点与点P所构成的三角形是等腰直角三角形,则n的值为____________.
【答案】(1)m=![]() ,n=
,n=![]() ;(2)见解析;(3)① B、D、E , ②2<m<3 , ③ 2或6
;(2)见解析;(3)① B、D、E , ②2<m<3 , ③ 2或6
【解析】
(1)把x=-![]() 和x=
和x=![]() 分别代入函数表达式,即可求得m,n;
分别代入函数表达式,即可求得m,n;
(2)按(1)的表格描点、连线即可;
(3)从函数图像上获取信息解答即可.
解:(1)把x=-![]() 和x=
和x=![]() 分别代入函数表达式,
分别代入函数表达式,
解得:y=![]() ,y=
,y=![]() :故答案为:
:故答案为:![]() ,
,![]() ;
;
(2)如图所示
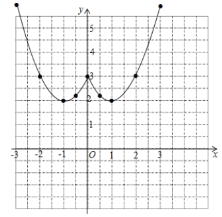
(3)
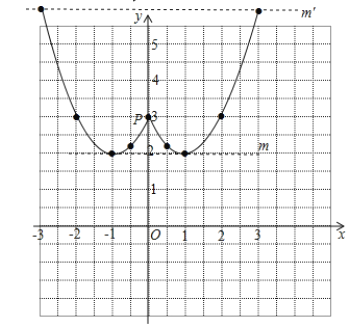
①A,如图:函数图像对称轴是直线x=0,故错误;
B.函数![]() 的图像有两个最低点,其坐标分别是(-1,2)、(1,2),故正确;C.当-1<x<1时,函数在y轴右侧,y随x的增大而减小,故错误;
的图像有两个最低点,其坐标分别是(-1,2)、(1,2),故正确;C.当-1<x<1时,函数在y轴右侧,y随x的增大而减小,故错误;
D.当函数![]() 的图像向下平移3个单位时,图像与x轴有三个公共点,正确;E.函数
的图像向下平移3个单位时,图像与x轴有三个公共点,正确;E.函数![]() 的图像,可以看作是函数
的图像,可以看作是函数![]() 的图像向右平移2个单位得到,正确;
的图像向右平移2个单位得到,正确;
故答案为:B,D、E;
②从图像看,2<m<3时,方程![]() 有四个解;
有四个解;
③如图,当直线y=n处于直线m或m1的位置时,点P和图像上的点构成等腰直角三角形,即n=2或6.

【题目】某地特产槟榔芋深受欢迎,某商场以7元/千克收购了3000千克优质槟榔芋,若现在马上出售,每千克可获得利润3元.根据市场调查发现,近段时间内槟榔芋的售价每天上涨0.2元/千克,为了获得更大利润,商家决定先贮藏一段时间后再出售.根据以往经验,这批槟榔芋的贮藏时间不宜超过100天,在贮藏过程中平均每天损耗约10千克.
(1)若商家将这批槟榔芋贮藏x天后一次性出售,请完成下列表格:
每千克槟榔芋售价(单位:元) | 可供出售的槟榔芋重量(单位:千克) | |
现在出售 | 3000 | |
x天后出售 |
(2)将这批槟榔芋贮藏多少天后一次性出售最终可获得最大利润?