题目内容
【题目】如图所示,四边形ABCD是矩形,把△ACD沿AC折叠到△ACD′,AD′与BC交于点E,若AD=4,DC=3,求BE的长. 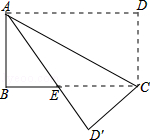
【答案】解:∵四边形ABCD为矩形, ∴AB=DC=3,BC=AD=4,AD∥BC,∠B=90°,
∵△ACD沿AC折叠到△ACD′,AD′与BC交于点E,
∴∠DAC=∠D′AC,
∵AD∥BC,
∴∠DAC=∠ACB,
∴∠D′AC=∠ACB,
∴AE=EC,
设BE=x,则EC=4﹣x,AE=4﹣x,
在Rt△ABE中,∵AB2+BE2=AE2 ,
∴32+x2=(4﹣x)2 , 解得x= ![]() ,
,
即BE的长为 ![]() .
.
【解析】根据矩形性质得AB=DC=3,BC=AD=4,AD∥BC,∠B=90°,再根据折叠性质得∠DAC=∠D′AC,而∠DAC=∠ACB,则∠D′AC=∠ACB,所以AE=EC, 设BE=x,则EC=4﹣x,AE=4﹣x,然后在Rt△ABE中利用勾股定理可计算出BE.

练习册系列答案
相关题目
【题目】阅读理解:由面积都是1的小正方格组成的方格平面叫做格点平面.而纵横两组平行线的交点叫做格点.如图1中,有9个格点,如果一个正方形的每个顶点都在格点上,那么这个正方形称为格点正方形. 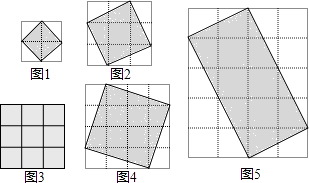
(1)探索发现:按照图形完成下表:
格点正方形边上格点数p | 格点正方形内格点数q |
| 格点正方形面积S | |
图1 | 4 | 1 | 2 | |
图2 | 4 | 4 | ||
图3 | 4 | 9 | ||
图4 | 4 |
关于格点正方形的面积S,从上述表格中你发现了什么规律?
(2)继续猜想:类比格点正方形的概念,如果一个长方形的每个顶点都在格点上,那么这个长方形称为格点长方形,对于格点长方形的面积,你认为也有类似(1)中的规律吗?试以图5中格点长方形为例来说明.