Question

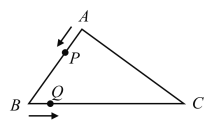
【题目】如图，在三角形中，，，．点从点出发以2个单位长度/秒的速度沿的方向运动，点从点沿的方向与点同时出发；当点第一次回到点时，点，同时停止运动；用（秒）表示运动时间．

（1）当为多少时，是的中点；

（2）若点的运动速度是个单位长度/秒，是否存在的值，使得；

（3）若点的运动速度是个单位长度/秒，当点，是边上的三等分点时，求的值．

Answer 1

【答案】（1）2；（2）存在，t=；（3）或

【解析】

（1）根据AB的长度和点P的运动速度可以求得；

（2）根据题意可得：当时，点P在AB上，点Q在BC上，据此列出方程求解即可；

（3）分两种情况：P为接近点A的三等分点，P为接近点C的三等分点，分别根据点的位置列出方程解得即可.

解：（1）∵，点P的运动速度为2个单位长度/秒，

∴当P为AB中点时，

（秒）；

（2）由题意可得：当时，

P，Q分别在AB，BC上，

∵点Q的运动速度为个单位长度/秒，

∴点Q只能在BC上运动，

∴BP=8-2t，BQ=t，

则8-2t=2×t，

解得t=，

当点P运动到BC和AC上时，不存在；

（3）当点P为靠近点A的三等分点时，如图，

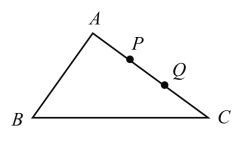
AB+BC+CP=8+16+8=32，

此时t=32÷2=16，

∵BC+CQ=16+4=20，

∴a=20÷16=，

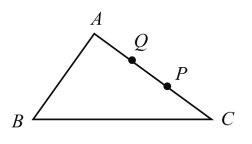
当点P为靠近点C的三等分点时，如图，

AB+BC+CP=8+16+4=28，

此时t=28÷2=14，

∵BC+CQ=16+8=24，

∴a=24÷14=.

综上：a的值为或.