题目内容
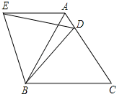
【题目】在等边△ABC中,D是边AC上一点,连接BD,将△BCD绕点B逆时针旋转60°,得到△BAE,连接ED,若BC=5,BD=4,则以下四个结论中: ①△BDE是等边三角形; ②AE∥BC; ③△ADE的周长是9; ④∠ADE=∠BDC.其中正确的序号是( )
A.②③④B.①②④C.①②③D.①③④
【答案】D
【解析】
先由△BCD绕点B逆时针旋转60°,得到△BAE得到BD=BE,∠DBE=60°,则可判断△BDE是等边三角形;根据等边三角形的性质得BA=BC,∠ABC=∠C=∠BAC=60°,再根据旋转的性质得到∠BAE=∠BCD=60°,∠BCD=∠BAE=60°,所以∠BAE=∠ABC=60°,则根据平行线的判定方法即可得到AE∥BC;根据等边三角形的性质得∠BDE=60°,而∠BDC>60°,则可判断∠ADE≠∠BDC;由△BDE是等边三角形得到DE=BD=4,再利用△BCD绕点B逆时针旋转60°,得到△BAE,则AE=CD,所以△AED的周长=AE+AD+DE=CD+AD+DE=AC+BD.
解:∵△BCD绕点B逆时针旋转60°,得到△BAE,
∴BD=BE,∠DBE=60°,
∴△BDE是等边三角形,所以①正确;
∵△ABC为等边三角形,
∴BA=BC,∠ABC=∠C=∠BAC=60°,
∵△BCD绕点B逆时针旋转60°,得到△BAE,
∴∠BAE=∠BCD=60°,∠BCD=∠BAE=60°,
∴∠BAE=∠ABC,
∴AE∥BC,所以②正确;
∴∠BDE=60°,
∵∠BDC=∠BAC+∠ABD>60°,
∴∠ADE≠∠BDC,所以④错误;
∵△BDE是等边三角形,
∴DE=BD=4,
而△BCD绕点B逆时针旋转60°,得到△BAE,
∴AE=CD,
∴△AED的周长=AE+AD+DE=CD+AD+DE=AC+4=5+4=9,所以③正确.
故选D.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案