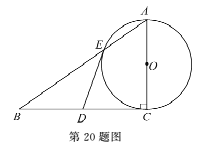
题目内容
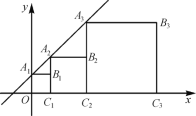
【题目】将正方形A1B1C1O,A2B2C2C1,A3B3C3C2按如图所示方式放置,点A1,A2,A3,…和点C1,C2,C3,…分别在直线![]() 和x轴上,则点B2019的横坐标是______.
和x轴上,则点B2019的横坐标是______.
【答案】![]() .
.
【解析】
利用一次函数图象上点的坐标特征及正方形的性质可得出点B1,B2,B3,B4,B5的坐标,根据点的坐标的变化可找出变化规律“点Bn的坐标为(2n-1,2n-1)(n为正整数)”,再代入n=2019即可得出结论.
当x=0时,y=x+1=1,
∴点A1的坐标为(0,1).
∵四边形A1B1C1O为正方形,
∴点B1的坐标为(1,1),点C1的坐标为(1,0).
当x=1时,y=x+1=2,
∴点A1的坐标为(1,2).
∵A2B2C2C1为正方形,
∴点B2的坐标为(3,2),点C2的坐标为(3,0).
同理,可知:点B3的坐标为(7,4),点B4的坐标为(15,8),点B5的坐标为(31,16),…,
∴点Bn的坐标为(2n-1,2n-1)(n为正整数),
∴点B2019的坐标为(22019-1,22018).
故答案为:22019-1.

练习册系列答案
相关题目
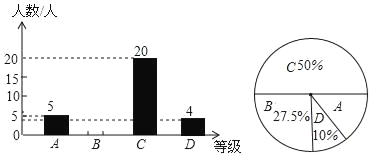
【题目】中央电视台的《朗读者》节目激发了同学们的读书热情,为了引导学生“多读书,读好书”,某校对八年级部分学生的课外阅读量进行了随机调查,整理调查结果发现,学生课外阅读的本数量少的有![]() 本,最多的有
本,最多的有![]() 本,并根据调查结果绘制了不完整的图表,如下所示:
本,并根据调查结果绘制了不完整的图表,如下所示:
本数(本) | 频数(人数) | 频率 |
|
|
|
|
|
|
|
|
|
|
|
|
合计 |
|
|

(![]() )统计图表中的
)统计图表中的![]() __________,
__________,![]() __________,
__________,![]() __________.
__________.
(![]() )请将频数分布直方图补充完整.
)请将频数分布直方图补充完整.
(![]() )求所有被调查学生课外阅读的平均本数.
)求所有被调查学生课外阅读的平均本数.
(![]() )若该校八年级共有
)若该校八年级共有![]() 名学生,请你估计该校八年级学生课外阅读
名学生,请你估计该校八年级学生课外阅读![]() 本及以上的人数.
本及以上的人数.