题目内容
24、如图，已知AB=AC，AD=AE，DE=BC，且∠BAD=∠CAE．求证：四边形BCED为矩形．
分析：要证明四边形BCED为矩形，则要证明四边形BCED是平行四边形，且对角线相等．
解答：证明：在△ABD和△ACE中，
因为AB=AC，AD=AE，∠BAD=∠CAE，
所以△ABD≌△ACE（SAS）
所以BD=CE又DE=BC．
所以四边形BCED为平行四边形．在△ACD和△ABE中，
因为AC=AB，AD=AE，∠CAD=∠CAB+∠BAD=∠CAB+∠CAE=∠BAE，
所以△ADC≌△AEB（SAS）所以CD=BE．
所以四边形BCED为矩形．（对角线相等的平行四边形是矩形）
因为AB=AC，AD=AE，∠BAD=∠CAE，
所以△ABD≌△ACE（SAS）
所以BD=CE又DE=BC．
所以四边形BCED为平行四边形．在△ACD和△ABE中，
因为AC=AB，AD=AE，∠CAD=∠CAB+∠BAD=∠CAB+∠CAE=∠BAE，
所以△ADC≌△AEB（SAS）所以CD=BE．
所以四边形BCED为矩形．（对角线相等的平行四边形是矩形）
点评：本题主要考查矩形的判定，证明对角线相等的平行四边形是矩形．
练习册系列答案
学而优衔接教材南京大学出版社系列答案
相关题目
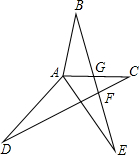如图，已知AB⊥AC，AD⊥AE，AB=AC，AD=AE，则∠BFD的度数是（ ）| A、60° | B、90° | C、45° | D、120° |
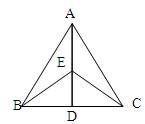10、如图，已知AB=AC，D是BC的中点，E是AD上的一点，图中全等三角形有几对（ ）
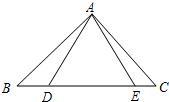26、如图，已知AB=AC，AD=AE．求证BD=CE．
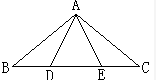2、如图，已知AB=AC，AD=AE，BD=EC，则图中有
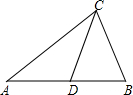如图，已知AB=AC，BC=CD=AD，求∠B的值．