题目内容
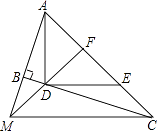
【题目】如图，MN是正方形ABCD的一条对称轴，点P是直线MN上的一个动点当PC+PD最小时，∠PCD=（ ）°．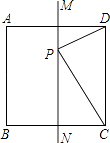 
A.60°
B.45°
C.30°
D.15°
【答案】B
【解析】解：连接BD交MN于P′，如图，
∵MN是正方形ABCD的一条对称轴，
∴P′B=P′C，
∴P′C+P′D=P′B+P′D=BD，
∴此时P′C+P′D最短，即点P运动到P′位置时，PC+PD最小，
∵点P′为正方形的对角线的交点，
∴∠P′CD=45°．
故选B．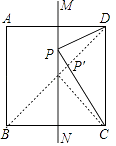
【考点精析】解答此题的关键在于理解正方形的性质的相关知识，掌握正方形四个角都是直角，四条边都相等；正方形的两条对角线相等，并且互相垂直平分，每条对角线平分一组对角；正方形的一条对角线把正方形分成两个全等的等腰直角三角形；正方形的对角线与边的夹角是45o；正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形，以及对轴对称-最短路线问题的理解，了解已知起点结点，求最短路径；与确定起点相反，已知终点结点，求最短路径；已知起点和终点，求两结点之间的最短路径；求图中所有最短路径．
新课标阶梯阅读训练系列答案
口算心算速算应用题系列答案
同步拓展阅读系列答案
【题目】自2014年12月28日北京公交地铁调价以来，人们的出行成本发生了较大的变化. 小林根据新闻，将地铁和公交车的票价绘制成了如下两个表格。（说明：表格中“6～12公里”指的是大于6公里，小于等于12公里，其他类似）
|
| ||||||||||||||||||||||||||||||
根据以上信息回答下列问题：
小林办了一张市政交通一卡通学生卡，目前乘坐地铁没有折扣。
（1）如果小林全程乘坐地铁的里程为14公里，用他的学生卡需要刷卡交费元；
（2）如果小林全程乘坐公交车的里程为16公里，用他的学生卡需要刷卡交元；
（3）小林用他的学生卡乘坐一段地铁后换乘公交车，两者累计里程为12公里。已知他乘坐地铁平均每公里花费0.4元，乘坐公交车平均每公里花费0.25元，此次行程共花费4.5元。请问小林乘坐地铁和公交车的里程分别是多少公里?
