题目内容
【题目】如图，平面直角坐标系中，四边形OABC是长方形，O为原点，点A在x轴上，点C在y轴上且A（10，0），C（0，6），点D在AB边上，将△CBD沿CD翻折，点B恰好落在OA边上点E处．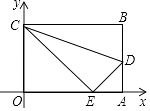 
（1）求点E的坐标；
（2）求折痕CD所在直线的函数表达式；
（3）请你延长直线CD交x轴于点F． ①求△COF的面积；
②在x轴上是否存在点P，使S△OCP= 
S△COF？若存在，求出点P的坐标；若不存在，请说明理由．
【答案】
（1）解：∵四边形ABCD是长方形，
∴BC=OA=10，∠COA=90°，
由折叠的性质知，CE=CB=10，
∵OC=6，
∴在直角△COE中，由勾股定理得OE= 
=8，
∴E（8，0）
（2）解：设CD所在直线的解析式为y=kx+b（k≠0），
∵C（0，6），
∴b=6，
设BD=DE=x，
∴AD=6﹣x，AE=OA﹣OE=2，
由勾股定理得AD2+AE2=DE2
即（6﹣x）2+22=x2，
解得x= 
，
∴AD=6﹣ = 
，
∴D（10， ），
代入y=kx+6 得，k=﹣ 
，
故CD所在直线的解析式为：y=﹣ x+6
（3）解：①在y=﹣ x+6中，令y=0，则x=18，
∴F（18，0），
∴△COF的面积= 
×OF×OC= ×18×6=54；
②在x轴上存在点P，使得S△OCP= S△COF，
设P（x，0），依题意得
×OP×OC= ×54，即 ×|x|×6=18，
解得x=±6，
∴在x轴上存在点P，使得S△OCP= S△COF，点P的坐标为（6，0）或（﹣6，0）．
【解析】（1）根据折叠的性质知CE=CB=10．在在直角△COE中，由勾股定理求得OE=8；（2）根据OC=6知C（0，6），由折叠的性质与勾股定理，求得D（10， ），利用待定系数法求CD所在直线的解析式；（3）①根据F（18，0），即可求得△COF的面积；②设P（x，0），依S△OCP= S△CDE得 ×OP×OC= ×54，即 ×|x|×6=18，求得x的值，即可得出点P的坐标．
【考点精析】解答此题的关键在于理解确定一次函数的表达式的相关知识，掌握确定一个一次函数，需要确定一次函数定义式y=kx+b（k不等于0）中的常数k和b．解这类问题的一般方法是待定系数法，以及对勾股定理的概念的理解，了解直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2．
