题目内容
【题目】如图，已知直线y=3x﹣3分别交x轴、y轴于A，B两点，抛物线y=x2+bx+c经过A，B两点，点C是抛物线与x轴的另一个交点（与A点不重合）．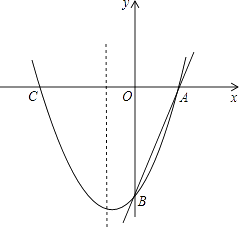
（1）求抛物线的解析式；
（2）求△ABC的面积；
（3）在抛物线的对称轴上，是否存在点M，使△ABM为等腰三角形？若不存在，请说明理由；若存在，求出点M的坐标．
【答案】
（1）
解：∵直线y=3x﹣3分别交x轴、y轴于A、B两点，
∴可得A（1，0），B（0，﹣3），
把A、B两点的坐标分别代入y=x2+bx+c得： 
，
解得： 
．
∴抛物线解析式为：y=x2+2x﹣3
（2）
解：令y=0得：0=x2+2x﹣3，
解得：x1=1，x2=﹣3，
则C点坐标为：（﹣3，0），AC=4，
故可得S△ABC= 
AC×OB= ×4×3=6
（3）
解：存在，理由如下：
抛物线的对称轴为：x=﹣1，假设存在M（﹣1，m）满足题意：
讨论：
①当MA=AB时，
∵OA=1，OB=3，
∴AB= 
，
，
解得： 
，
∴M1（﹣1， 
），M2（﹣1，﹣ ）；
②当MB=BA时， 
，
解得：M3=0，M4=﹣6，
∴M3（﹣1，0），M4（﹣1，﹣6）（不合题意舍去），
③当MB=MA时， 
，
解得：m=﹣1，
∴M5（﹣1，﹣1），
答：共存在4个点M1（﹣1， ），M2（﹣1，﹣ ），M3（﹣1，0），M4（﹣1，﹣1）使△ABM为等腰三角形
【解析】（1）根据直线解析式求出点A及点B的坐标，然后将点A及点B的坐标代入抛物线解析式，可得出b、c的值，求出抛物线解析式；（2）由（1）求得的抛物线解析式，可求出点C的坐标，继而求出AC的长度，代入三角形的面积公式即可计算；（3）根据点M在抛物线对称轴上，可设点M的坐标为（﹣1，m），分三种情况讨论，①MA=BA，②MB=BA，③MB=MA，求出m的值后即可得出答案．
【考点精析】通过灵活运用二次函数的图象和二次函数的性质，掌握二次函数图像关键点：1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点；增减性：当a>0时，对称轴左边，y随x增大而减小；对称轴右边，y随x增大而增大；当a<0时，对称轴左边，y随x增大而增大；对称轴右边，y随x增大而减小即可以解答此题．
