题目内容
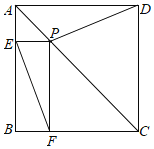
【题目】(1)如图1,长方形ABCD中分别沿AF、CE将AC两侧折叠,使点B、D分别落在AC上的G、H处,则线段AE______CF.(填“>”“<”或“=”)
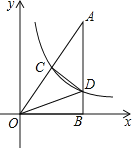
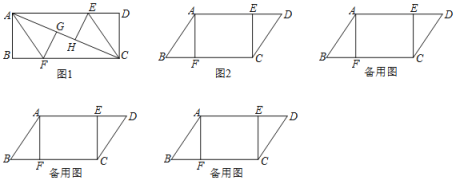
(2)如图2,在平行四边形ABCD中,△ABF≌△CDE,AB=10cm,BF=6cm,AF=8cm,动点P、Q分别从A、C两点同时出发,点P自A→F→B→A停止,点Q自C→D→E→C停止.
①若点P的速度为每秒5cm,点Q的速度为每秒4cm,设运动时间为t秒.当点P在FB上运动,而点Q在DE上运动时,若四边形APCQ是平行四边形,求此时t的值.
②若点P、Q的运动路程分别为a、b(单位:cm,ab≠0),利用备用图探究,当a与b满足什么数量关系时,四边形APCQ是平行四边形.
【答案】(1)=;(2)①![]() 秒;②a+b=24(ab≠0)
秒;②a+b=24(ab≠0)
【解析】
(1)根据内错角相等得出AF∥CE,由两对应边互相平行得出AFCE是平行四边形,即可得出AE=CF;
(2)①当P点在BF上,Q点在ED上时,能构成平行四边形,根据平行四边形的性质,列出方程求解即可;
②分三种情况:当点P在AF上,Q点在CE上时,AP=CQ;当点P在BF上,Q点在DE上时,AQ=CP;当点P在AB上,Q点在CD上时,AP=CQ,分别得出a与b满足的数量关系式.
解:(1)如图1,∵四边形ABCD是矩形,
∴AD∥BC,
∴∠BAC=∠DCA,
由折叠的性质可知,∠FAC=![]() ∠BAC=
∠BAC=![]() ∠DCA=∠ECA,
∠DCA=∠ECA,
∴AF∥CE,
∴四边形AFCE是平行四边形,
∴AE=CF.
故答案为:=;
(2)①∵在平行四边形ABCD中,△ABF≌△CDE,
∴AE=CF,BF=DE=6cm,AB=CD=10cm,
∵如图2,当P点在BF上,Q点在ED上,以A、C、P、Q四点为顶点的四边形是平行四边形时,PC=QA,
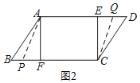
∴FP=EQ,
∵点P的速度为每秒5cm,点Q的速度为每秒4cm,运动时间为t秒,
∴PF=5t-8,QE=16-4t,
∴5t-8=16-4t,
解得t=![]() ,
,
∴以A、C、P、Q四点为顶点的四边形是平行四边形时,t=![]() 秒;
秒;
②由题意得,以A,C,P,Q四点的四边形是平行四边形时,点P、Q在相互平行的对边上,
分三种情况:
Ⅰ.如图3,当点P在AF上,Q点在CE上时,AP=CQ,
即a=24-b,得:a+b=24;
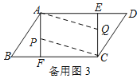
Ⅱ.如图4,当点P在BF上,Q点在DE上时,AQ=CP,
又∵AE=CF,
∴EQ=FP,
即16-b=a-8,得a+b=24;
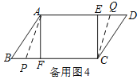
Ⅲ.如图5,当点P在AB上,Q点在CD上时,AP=CQ,
即24-a=b,得a+b=24.
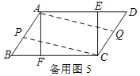
综上所述,a与b满足的数量关系式是a+b=24(ab≠0).

 名校课堂系列答案
名校课堂系列答案