题目内容
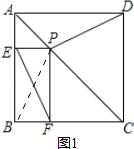
【题目】如图,P为正方形ABCD的对角线上任一点,PE⊥AB于E,PF⊥BC于F.
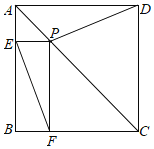
(1)判断DP与EF的关系,并证明;
(2)若正方形ABCD的边长为6,∠ADP:∠PDC=1:3.求PE的长.
【答案】(1)DP=EF,且DP⊥EF,理由见解析;(2)6﹣3![]()
【解析】
(1)如图1,连接PB,由正方形的性质得到BC=DC,∠BCP=∠DCP,接下来证明△CBP≌△CDP,于是得到DP=BP,然后证明四边形BFPE是矩形,由矩形的对角线相等可得到BP=EF,从而等量代换可证得DP=EF;如图2,延长DP交EF于G,延长EP交CD于H,连接PB,由△CBP≌△CDP,依据全等三角形对应角相等可得到∠CDP=∠CBP,由四边形EPFB是矩形可证明∠CBP=∠FEP,从而得到∠HDP=∠FEP,由∠DPH+∠PDH=90°可证明∠EPG+∠PEG=90°,从而可得到DP⊥EF;
(2)先根据勾股定理计算AC,根据∠ADP:∠PDC=1:3和三角形内角和定理可得∠CPD=∠CDP,计算AP,由△AEP是等腰直角三角形,可得PE的长.
解:(1)DP=EF,且DP⊥EF,理由是:
如图1所示:连接PB,
∵四边形ABCD是正方形,
∴BC=DC,∠BCP=∠DCP=45°,
∵在△CBP和△CDP中,
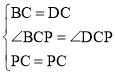 ,
,
∴△CBP≌△CDP(SAS),
∴DP=BP,
∵PE⊥AB,PF⊥BC,
∴∠PEB=∠ABC=∠PFB=90°,
∴四边形BFPE是矩形,
∴BP=EF,
∴DP=EF;
如图2所示:延长DP交EF于G,延长EP交CD于H,连接PB.
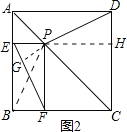
∵△CBP≌△CDP,
∴∠CDP=∠CBP,
∵四边形BFPE是矩形,
∴∠CBP=∠FEP,
∴∠CDP=∠FEP,
又∵∠EPG=∠DPH,
∴∠EGP=∠DHP,
∵PE⊥AB,AB∥DC,
∴PH⊥DC.即∠DHP=90°,
∴∠EGP=∠DHP=90°,
∴PG⊥EF,即DP⊥EF;
(2)Rt△ADC中,AD=CD=6,
∴AC=![]() =6
=6![]() ,
,
∵∠ADP:∠PDC=1:3,∠ADC=90°,
∴∠CDP=67.5°,
∵∠DCP=45°,
∴∠CPD=180°﹣45°﹣67.5°=67.5°,
∴∠CPD=∠CDP,
∴PC=CD=6,
∴AP=6![]() ﹣6,
﹣6,
∵∠EAP=45°,∠AEP=90°,
∴△AEP是等腰直角三角形,
∴PE=![]() =6﹣3
=6﹣3![]() .
.