题目内容
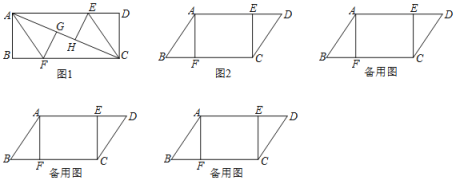
【题目】如图,在平行四边形ABCD中,AB=6cm,AD=10cm,点P在AD边上以每秒1cm的速度从点A向点D运动,点Q在BC边上以每秒4cm的速度从点C出发,在CB间往返运动,两个点同时出发,当点P到达点D时停止运动,同时点Q也停止运动.设运动时间为ts,当t为何值时,以P,D,Q,B为顶点的四边形是平行四边形?

【答案】当运动时间为0秒或4秒或![]() 秒或8秒时,以P、D、Q、B四点组成的四边形为平行四边形
秒或8秒时,以P、D、Q、B四点组成的四边形为平行四边形
【解析】
由四边形ABCD为平行四边形可得出PD∥BQ,结合平行四边形的判定定理可得出当PD=BQ时以P、D、Q、B四点组成的四边形为平行四边形,分四种情况考虑,在每种情况中由PD=BQ即可列出关于t的一元一次方程,解之即可得出结论.
解:∵四边形ABCD为平行四边形,
∴PD∥BQ.
若要以P、D、Q、B四点组成的四边形为平行四边形,则PD=BQ.
设运动时间为t.
当0≤t≤![]() 时,AP=t,PD=10﹣t,CQ=4t,BQ=10﹣4t,
时,AP=t,PD=10﹣t,CQ=4t,BQ=10﹣4t,
∴10﹣t=10﹣4t,
3t=0,
∴t=0;
当![]() <t≤5时,AP=t,PD=10﹣t,BQ=4t﹣10,
<t≤5时,AP=t,PD=10﹣t,BQ=4t﹣10,
∴10﹣t=4t﹣10,
解得:t=4;
当5<t≤![]() 时,AP=t,PD=10﹣t,CQ=4t﹣20,BQ=30﹣4t,
时,AP=t,PD=10﹣t,CQ=4t﹣20,BQ=30﹣4t,
∴10﹣t=30﹣4t,
解得:t=![]() ;
;
当![]() <t≤10时,AP=t,PD=10﹣t,BQ=4t﹣30,
<t≤10时,AP=t,PD=10﹣t,BQ=4t﹣30,
∴10﹣t=4t﹣30,
解得:t=8.
综上所述:当运动时间为0秒或4秒或![]() 秒或8秒时,以P、D、Q、B四点组成的四边形为平行四边形.
秒或8秒时,以P、D、Q、B四点组成的四边形为平行四边形.

练习册系列答案
相关题目