��Ŀ����
����Ŀ��ij��˾�з�������560���²�Ʒ��Ҫ���ӹ������Ͷ���г������ɼס��������������ӹ���������֪����ÿ��ӹ��������²�Ʒ�������ҹ���ÿ��ӹ������²�Ʒ������1.5�������Ҽӹ�����240���²�Ʒ�������ҹ�������4�죮
��1����ס�����������ÿ��ֱ�ɼӹ��������ټ��²�Ʒ��
��2��������ÿ��ļӹ������ɱ�Ϊ2.8��Ԫ���ҹ���ÿ��ļӹ������ɱ�Ϊ2.4��ԪҪʹ�����²�Ʒ�ļӹ������ܳɱ�������60��Ԫ������Ӧ���ż����ӹ����������죿
���𰸡���1���ס�����������ÿ��ֱ�ɼӹ�����30����20���²�Ʒ����2��Ӧ���ż����ӹ�����9�죮
��������
��1�����ҹ���ÿ��ɼӹ�����x���²�Ʒ�������ÿ��ɼӹ�����1.5x���²�Ʒ�����������г����̣�������̵Ľ⼴�ɵõ������
��2��������ӹ�����y�죬���������г�����ʽ���������ʽ�Ľ⼯���ɵõ������
�⣺��1�����ҹ���ÿ��ɼӹ�����x���²�Ʒ�������ÿ��ɼӹ�����1.5x���²�Ʒ��
��������ã�![]() ��
��
ȥ��ĸ�ã�240+6x��360��
��ã�x��20��
������x��20�Ƿ�ʽ���̵Ľ⣬�ҷ������⣬
��1.5x��30��
��ס�����������ÿ��ֱ�ɼӹ�����30����20���²�Ʒ��
��2��������ӹ�����y�죬
��������ã�2.8y+2.4��![]() ��60��
��60��
��ã�y��9��
������Ӧ���ż����ӹ�����9�죮

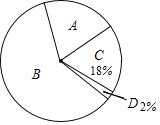
����Ŀ��ij��ѧ��һ����ѧ��ȤС���ڱ�Уѧ���п�չ������Ϊ������֪��������ר�������������ȡ��������ķ�ʽ�����ʾ����飬�ʾ�����Ľ����Ϊ��A���dz��˽�������B���Ƚ��˽�������C�������˽�������D����̫�˽����ĸ��ȼ������������ݽ����������Ƴ�����������������ͳ��ͼ����������ͼ���е���Ϣ�����������
�ȼ� | A | B | C | D |
Ƶ�� | 40 | 120 | 36 | n |
Ƶ�� | 0.2 | m | 0.18 | 0.02 |
��1������m���� ����n���� ����
��2������ͳ��ͼ�У�A��������Ӧ�����ε�Բ�Ľ����� ����������ȡѧ���Զ������˽�̶ȵ��������� ����
��3������У����ѧ��1500�ˣ�����ݵ�����������Щѧ�������Ƚ��˽�������ԼΪ���٣�