题目内容
【题目】如图,已知一张长方形纸片,![]() ,
,![]() (
(![]() ).将这张纸片沿着过点
).将这张纸片沿着过点![]() 的折痕翻折,使点
的折痕翻折,使点![]() 落在
落在![]() 边上的点
边上的点![]() ,折痕交
,折痕交![]() 于点
于点![]() ,将折叠后的纸片再次沿着另一条过点
,将折叠后的纸片再次沿着另一条过点![]() 的折痕翻折,点
的折痕翻折,点![]() 恰好与点
恰好与点![]() 重合,此时折痕交
重合,此时折痕交![]() 于点
于点![]() .
.
(1)在图中确定点![]() 、点
、点![]() 和点
和点![]() 的位置;
的位置;
(2)联结![]() , 则
, 则![]() 等于多少°;
等于多少°;
(3)用含有![]() 、
、![]() 的代数式表示线段
的代数式表示线段![]() 的长.
的长.
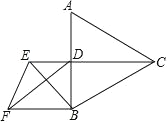
【答案】(1)点F、点E和点G的位置如图所示;见解析;(2)45;(3)![]() .
.
【解析】
依题意先画出图形,再利用折叠的性质来得出等量关系,依次求解.
(1)点F、点E和点G的位置如图所示;
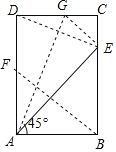
(2)由折叠的性质得:∠DAE=∠EAB,
∵四边形ABCD是矩形,
∴∠BAD=∠DAE+∠EAB=90°,
∴∠EAB=45°;
(3)由折叠的性质得:DG=EG,
∵∠ABE=90°,∠EAB=45°,
∴∠AEB=45°,
∴BE=AB=a,
∴CE=b-a,
设CG=x,则DG=EG=a-x,
在Rt△CEG中,CG2+CE2=EG2,
即x2+(b-a)2=(a-x)2,
解得:x=![]() ,
,
∴DG=a-x=a-![]() =a-b+
=a-b+![]() .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目