题目内容
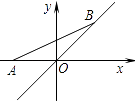
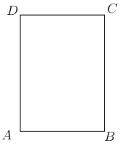
【题目】如图1,A(m,0),B(0,n),且m,n满足(m﹣2)2![]() 0.
0.
(1)求S△ABO;
(2)点C为y轴负半轴上一点,BD⊥CA交CA的延长线于点D,若∠BAD=∠CAO,求![]() 的值;
的值;
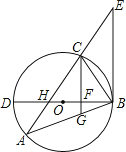
(3)点E为y轴负半轴上一点,OH⊥AE于H,HO,AB的延长线交于点F,G为y轴正半轴上一点,且BG=OE,FG,EA的延长线交于点P,求证:点P的纵坐标是定值.

【答案】(1)2;(2)![]() ;(3)1
;(3)1
【解析】
(1)利用非负性得出m,n值,即可得出点A,B坐标,最后用三角形的面积公式即可;
(2)先求出先求出OC,进而得出22.5°的正切值,再求出AC的平方,再求出BD的平方即可;
(3)设出点E坐标,用待定系数法和直线交点坐标即可确定出点P坐标即可得出结论.
(1)∵(m﹣2)2![]() 0,∴m=n=2,∴A(2,0),B(0,2),∴OA=2,OB=2,∴S△AOB
0,∴m=n=2,∴A(2,0),B(0,2),∴OA=2,OB=2,∴S△AOB![]() OA×OB=2;
OA×OB=2;
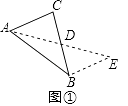
(2)如图1,在OC上取一点E,使OE=OA=2,由(1)知,OA=OB=2,∴∠OAB=45°,∴AE=2![]() .
.
∵∠BAD=∠CAO,∴∠BAD=∠CAO=67.5°.
∵∠ADB=∠AOC=90°,∴∠ABD=∠ACO=22.5°,∴CE=AE=2![]() ,∴OC=OE+CE=2(
,∴OC=OE+CE=2(![]() 1),∴AC2=OA2+OC2=4+4(
1),∴AC2=OA2+OC2=4+4(![]() 1)2=8(2
1)2=8(2![]() ),tan∠ACO
),tan∠ACO![]() 1.
1.
在Rt△ABD中,tan∠ABD=tan22.5°=tan∠ACO![]() 1,∴AD=(
1,∴AD=(![]() 1)BD.
1)BD.
在Rt△AOB中,OA=OB=2,∴AB=2![]() ,根据勾股定理得:AD2+BD2=AB2,∴[(
,根据勾股定理得:AD2+BD2=AB2,∴[(![]() 1)BD]2+BD2=8,∴BD2=2(2
1)BD]2+BD2=8,∴BD2=2(2![]() ),
),![]() ,∴
,∴![]() ;
;
(3)如图2,由(1)知,A(2,0),B(0,2),∴直线AB解析式为y=﹣x+2①,设E(0,a),∴OE=|a|=﹣a.
∵BG=OE,∴BG=﹣a,∴OG=2﹣a,∴G(0,2﹣a).
∵A(2,0),E(0,a),∴直线AE解析式为y![]() x+a②.
x+a②.
∵OH⊥AE,∴直线OH解析式为y![]() x③,联立①③得:x
x③,联立①③得:x![]() ,y
,y![]() ,∴F(
,∴F(![]() ).
).
∵G(0,2﹣a),∴直线FG的解析式为y![]() x+2﹣a④,联立②④得:x
x+2﹣a④,联立②④得:x![]() ,y=1,∴P(
,y=1,∴P(![]() ,1),∴点P的纵坐标是定值,定值为1.
,1),∴点P的纵坐标是定值,定值为1.

 阅读快车系列答案
阅读快车系列答案