题目内容
【题目】如图，正方形AOCB的边长为4，反比例函数y= 
（k≠0，且k为常数）的图象过点E，且S△AOE=3S△OBE ． 
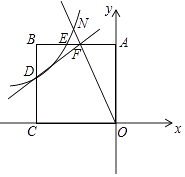
（1）求k的值；
（2）反比例函数图象与线段BC交于点D，直线y= 
x+b过点D与线段AB交于点F，延长OF交反比例函数y= （x＜0）的图象于点N，求N点坐标．
【答案】
（1）解：∵S△AOE=3S△OBE，
∴AE=3BE，
∴AE=3，
∴E（﹣3，4）
反比例函数y= 
（k≠0，且k为常数）的图象过点E，
∴4= 
，即k=﹣12
（2）解：∵正方形AOCB的边长为4，
∴点D的横坐标为﹣4，点F的纵坐标为4．
∵点D在反比例函数的图象上，
∴点D的纵坐标为3，即D（﹣4，3）．
∵点D在直线y= 
x+b上，
∴3= ×（﹣4）+b，解得b=5．
∴直线DF为y= x+5，
将y=4代入y= x+5，得4= x+5，解得x=﹣2．
∴点F的坐标为（﹣2，4），
设直线OF的解析式为y=mx，
代入F的坐标得，4=﹣2m，
解得m=﹣2，
∴直线OF的解析式为y=﹣2x，
解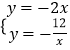 
，得 
．
∴N（﹣ 
，2 ）
【解析】（1）根据题意求得E的坐标，把点E（﹣3，4）代入利用待定系数法即可求出k的值；（2）由正方形AOCB的边长为4，故可知点D的横坐标为﹣4，点F的纵坐标为4．由于点D在反比例函数的图象上，所以点D的纵坐标为3，即D（﹣4，3），由点D在直线y= x+b上可得出b的值，进而得出该直线的解析式，再把y=4代入直线的解析式即可求出点F的坐标，然后根据待定系数法求得直线OF的解析式，然后联立方程解方程组即可求得．
【考点精析】掌握正方形的性质是解答本题的根本，需要知道正方形四个角都是直角，四条边都相等；正方形的两条对角线相等，并且互相垂直平分，每条对角线平分一组对角；正方形的一条对角线把正方形分成两个全等的等腰直角三角形；正方形的对角线与边的夹角是45o；正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形．
