题目内容
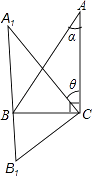
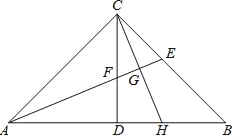
【题目】如图,在△ABC中,∠ACB=90°,AC=BC,△ABC的高CD与角平分线AE相交点F,过点C作CH⊥AE于G,交AB于H.下列说法:①∠BCH=∠CAE;②DF=EF;③CE=BH;④S△ABE=2S△ACE;⑤CF=![]() DF.正确的是_____.
DF.正确的是_____.
【答案】①③⑤
【解析】
①根据同角的余角相等可得结论正确;
②如图1,作辅助线,构建三角形的内心为F,根据角平分线的性质得:DF=FM,由垂线段最短可知:EF>FM,则EF>DF;
③如图1,证明△ACF≌△CBH,可得CF=BH=CE,可作判断;
④如图2,连接EH,FH,先证明四边形CFHE是菱形,得CD∥EH,则EH⊥AB,所以△EHB是等腰直角三角形,则BE=![]() EH=
EH=![]() CE,根据三角形面积公式可得S△ABE=
CE,根据三角形面积公式可得S△ABE=![]() S△ACE;
S△ACE;
⑤如图2,易得△ADF≌△CDH,由△FDH是等腰直角三角形,则FH=![]() DF,所以CF=FH=
DF,所以CF=FH=![]() DF.
DF.
①∵∠ACB=90°,
∴∠CAE+∠AEC=90°,
∵CH⊥AE,
∴∠CGE=90°,
∴∠BCH+∠AEC=90°,
∴∠BCH=∠CAE;
故①正确;
②如图1,连接FB,过F作FM⊥BC于M,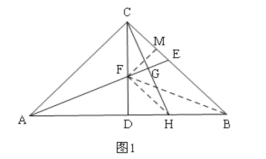
∵AC=BC,CD⊥AB,
∴CD平分∠ACB,
∵AE平分∠CAB,
∴BF平分∠ABC,
∵FD⊥AB,
∴DF=FM,
Rt△FME中,∠AEC=45°+22.5°=67.5°,
∴EF>FM,
即EF>DF,
故②不正确;
③如图1,∵∠DCH=∠BCH,AE⊥CG,
∴∠CFG=∠CEF,
∴CF=CE,
在△ACF和△CBH中,
∵∠HCB=∠FAC,BC=AC,∠B=∠ACF=45°,
∴△ACF≌△CBH,
∴CF=BH=CE,
故③正确;
④如图2,连接EH,FH,
∵∠AHC=∠B+∠BCH=45°+22.5°=67.5°,
∠ACH=90°∠BCH=67.5°,
∴∠AHC=∠ACH,
∴AC=AH,
∵AE⊥CH,
∴CG=GH,
∵CF=CE,
∴GF=GE,
∴四边形CFHE是菱形,
∴CD∥EH,
∵CD⊥AB,
∴EH⊥AB,
∴△EHB是等腰直角三角形,
∴BE=![]() EH=
EH=![]() CE,
CE,
∵S△ABE=![]() BEAC,
BEAC,
S△ACE=![]() CEAC,
CEAC,
∴S△ABE=![]() S△ACE,
S△ACE,
故④不正确;
⑤如图2,易得△ADF≌△CDH,
∴DF=DH,
∴∠FHD=45°,
∴△FDH是等腰直角三角形,
∴FH=![]() DF,
DF,
∵∠AHC=67.5°,
∴∠FHC=∠FCH=22.5°,
∴CF=FH=![]() DF,
DF,
故⑤正确;
综上所述,正确的是:①③⑤
故答案为:①③⑤.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案