Question

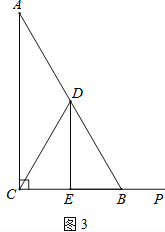
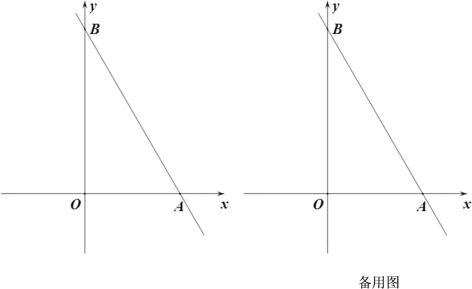
【题目】如图，在平面直角坐标系xOy中，直线：交轴于点、交轴于点，

（1）求直线的函数表达式；

（2）设点是轴上的一点

①在坐标平面内是否存在点，使以、、、为顶点的四边形是菱形？若存在，求出点的坐标；若不存在，说明理由．

②若是线段的中点，点与点关于轴对称，点在直线上，当为等边三角形时，求直线的函数表达式.

Answer 1

【答案】（1）；（2） ， ， ；（3）或

【解析】

（1）将点A的坐标代入直线：中即可求出直线的解析式；

（2）①先假设存在点Q，则以A,P,B,Q为顶点的四边形是菱形，再利用菱形的性质求点Q的坐标即可，如果能求出来，说明存在，反之则不存在；

②要求DM的直线必须知道点M的坐标，求点M的坐标必须把它放到直角三角形中去求.利用关于y轴对称的点的特点和等边三角形的性质，结合全等三角形及锐角三角函数解题即可.

解：（1）将代入得，

，

解得

所以，直线的函数表达式为；

（2）①直线l中，令x=0,y=,∴OB=

由勾股定理得

若AP为对角线时，有两种情况：

∵BP∥AQ

∴Q点与A点横坐标相同

∵四边形ABPQ是菱形

∴AQ=AB=8

若点P在点B上端，则Q的坐标为（4,8）

若点P在点B下端，则Q的坐标为（4,-8）

若AB为对角线

∵四边形APBQ为菱形

设AB,PQ交于点D

∴AB⊥PQ，

∴tan∠OBA=

∴∠OBA=30°

∵PB∥AQ

∴∠BAQ=30°

在Rt△ADQ中，

∴

∴Q的坐标为

若BP为对角线

∵四边形ABQP为菱形

∴BP⊥AQ,AO=OQ

∴Q的坐标为

综上所述，这样的Q点有4个，分别是

， ，

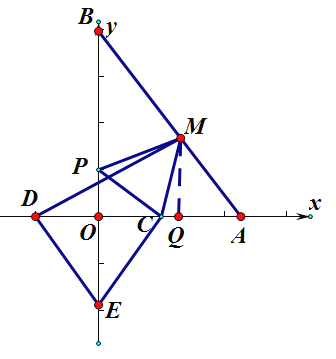
②点D与C点关于y轴对称，所以D的坐标为（-2,0）

如图，当点在轴上方时，

将及CD边绕点逆时针旋转至点与点重合，设与重合，则，，作MQ⊥AD于点Q

∵CD=CE,

∴为等边三角形

∴点在的中垂线上，即在轴上，于是

∵∠MCP=∠DCE=60°

∴∠MCP+∠PCD=∠DCE+∠PCD

∴∠MCD=∠PCE

在△MCD和△PCE中

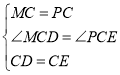
∴△MCD≌△PCE（SAS）

∴

在Rt△AMQ中，

∵∠BAO=60°

∴tan60°=

设AQ=x,则MQ=

在Rt△DMQ中，

解得

∴

∴

设DM的直线方程为

将D（-2,0），代入直线方程中

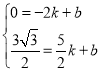解得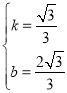

所以，直线DM的函数表达式为

当点在轴下方时，同理可得直线的函数表达式为