题目内容
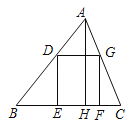
【题目】如图,四边形DEFG是△ABC的内接正方形,D、G分别在AB、AC上,E、F在BC上,AH是△ABC的高,已知BC=20,AH=16,求正方形DEFG的边长.
【答案】![]()
【解析】
由正方形的性质得DG∥EF,相似三角形的判定与性质求出△ADG∽△ABC,![]() ,再由平行线间的距离,线段的和差和一元一次方程的应用求出正方形DEFG的边长为
,再由平行线间的距离,线段的和差和一元一次方程的应用求出正方形DEFG的边长为![]() .
.
如图所示: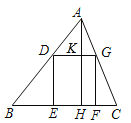
∵四边形DEFG是正方形,
∴DG∥EF,DG=DE,
∴△ADG∽△ABC,
∴![]() ,
,
∵BC=20,AH=16,
∴![]() ,
,
又∵AH是△ABC的高,
∴DE=KH,
∴DG=DE=KH,
∴![]() ,
,
设AK=4x,则KH=5x,
∵AH=AK+KH,
∴4x+5x=16,
解得:x=![]() ,
,
∴KH=DG=5x=![]() ,
,
即正方形DEFG的边长为![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目