题目内容
【题目】在矩形ABCD中,AB=2,∠ACB=30°,将矩形ABCD绕点A逆时针方向旋转,得到矩形AB′C′D′,记旋转角为α(0<α<90°).
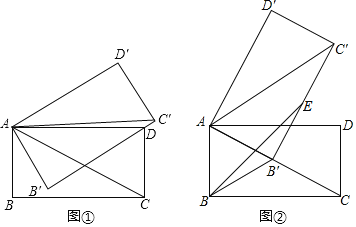
(I)如图①,当B'C'过点D时,求△ADC'的面积S的值;
(Ⅱ)如图②,当点B的对应点B'落在AC上时,在B′C′上取点E,使B'E=AB.
①求∠EBB'的大小;
②求BE的长(直接写出结果即可).
【答案】(Ⅰ)S△ADC′=2![]() ﹣2
﹣2![]() ;(Ⅱ)①∠BEB′=15°;②BE=
;(Ⅱ)①∠BEB′=15°;②BE=![]()
![]() .
.
【解析】
(Ⅰ)如图①中,解直角三角形求出DB′,根据S△ADC′=S△AB′C′﹣S△ADB′,计算即可.
(Ⅱ)①证明△ABB′是等边三角形,利用圆周角定理即可解决问题.
②如图②中,作EH⊥BB′交BB′于H.解直角三角形求出EH,BH,利用勾股定理即可解决问题.
解:(Ⅰ)如图①中,
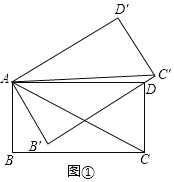
在Rt△ABC中,∵∠B=90°,AB=2,∠ACB=30°,
∴AC=2AB=4,![]() ,
,
在Rt△ADB′中,![]() ,
,
∴![]()
(Ⅱ)①如图②中,连接AE.
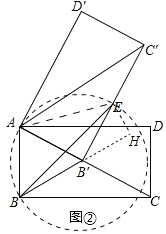
∵AB=AB′,∠BAB′=60°,
∴△ABB′是等边三角形,
∴B′A=B′B=B′E,∠AB′B=60°,
∴点B′是△ABE的外接圆的圆心,
∴![]() ,
,
∵∠AB′E=90°,B′A=B′E,
∴∠AEB′=45°,
∴∠BEB′=45°﹣30°=15°.
②如图②中,作EH⊥BB′交BB′于H.
∵B′E=B′B,
∴∠B′BE=∠B′EB=15°,
∴∠EB′H=30°,
∴EH=![]() EB′=1,HB′=
EB′=1,HB′=![]() ,
,
∴![]() .
.

练习册系列答案
相关题目