ÌâÄżÄÚÈĘ
ĄŸÌâÄżĄżÒŃÖȘŁșŸŰĐÎ![]() ÖĐŁŹ
ÖĐŁŹ![]() ŁŹ
ŁŹ![]() ŁŹ”ă
ŁŹ”ă![]() ÊǶԜÇÏß
ÊǶԜÇÏß![]() ÉÏ”ÄÒ»žö¶Ż”㣏ÁŹœÓ
ÉÏ”ÄÒ»žö¶Ż”㣏ÁŹœÓ![]() ŁŹÒÔ
ŁŹÒÔ![]() ÎȘ±ßÔÚ
ÎȘ±ßÔÚ![]() ”ÄÓÒČàŚś”ȱß
”ÄÓÒČàŚś”ȱß![]() Łź
Łź
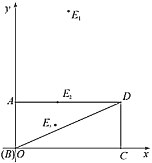
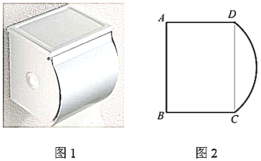
Łš1Ł©ąÙÈçÍŒ1ŁŹ”±”ă![]() Ô˶Ż”œÓë”ă
Ô˶Ż”œÓë”ă![]() ÖŰșÏʱŁŹŒÇ”ȱß
ÖŰșÏʱŁŹŒÇ”ȱß![]() ÎȘ”ȱß
ÎȘ”ȱß![]() ŁŹÔò”ă
ŁŹÔò”ă![]() ”œ
”œ![]() ”ÄŸàÀëÊÇ________Ł»
”ÄŸàÀëÊÇ________Ł»
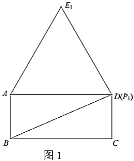
ąÚÈçÍŒ2ŁŹ”±”ă![]() Ô˶Ż”œ”ă
Ô˶Ż”œ”ă![]() ÂäÔÚ
ÂäÔÚ![]() ÉÏʱŁŹŒÇ”ȱß
ÉÏʱŁŹŒÇ”ȱß![]() ÎȘ”ȱß
ÎȘ”ȱß![]() .Ôò”ȱß
.Ôò”ȱß![]() ”ı߳€
”ı߳€![]() ÊÇ________Ł»
ÊÇ________Ł»
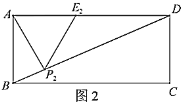
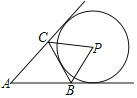
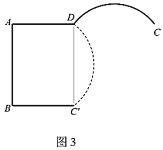
Łš2Ł©ÈçÍŒ3ŁŹ”±”ă![]() Ô˶Ż”œÓë”ă
Ô˶Ż”œÓë”ă![]() ÖŰșÏʱŁŹŒÇ”ȱß
ÖŰșÏʱŁŹŒÇ”ȱß![]() ÎȘ”ȱß
ÎȘ”ȱß![]() ŁŹčę”ă
ŁŹčę”ă![]() Śś
Śś![]() œ»
œ»![]() ÓÚ”ă
ÓÚ”ă![]() ŁŹÇó
ŁŹÇó![]() ”Äł€Ł»
”Äł€Ł»
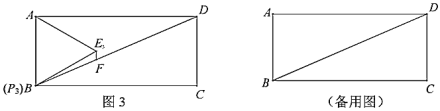
Łš3Ł©ąÙÔÚÉÏÊö±ä»ŻčęłÌÖДĔă![]() ŁŹ
ŁŹ![]() ŁŹ
ŁŹ![]() ÊÇ·ńÔÚÍŹÒ»Ö±ÏßÉÏŁżÇ뜚ÁąÆœĂæÖ±œÇŚű±êÏ”ŒÓÒÔĆĐ¶ÏŁŹČąË”ĂśÀíÓÉŁź
ÊÇ·ńÔÚÍŹÒ»Ö±ÏßÉÏŁżÇ뜚ÁąÆœĂæÖ±œÇŚű±êÏ”ŒÓÒÔĆĐ¶ÏŁŹČąË”ĂśÀíÓÉŁź
ąÚ”ă![]() ”ÄλÖĂËæŚĆ¶Ż”ă
”ÄλÖĂËæŚĆ¶Ż”ă![]() ÔÚÏ߶Î
ÔÚÏ߶Î![]() ÉÏ”ÄλÖñ仯¶ű±ä»ŻŁŹČÂÏëčŰÓÚËùÓĐ”ă
ÉÏ”ÄλÖñ仯¶ű±ä»ŻŁŹČÂÏëčŰÓÚËùÓĐ”ă![]() ”ÄλÖĂ”ÄÒ»žöÊęѧœáÂÛŁŹÊÔÓĂÒ»Ÿä»°±íÊöŁș______Łź
”ÄλÖĂ”ÄÒ»žöÊęѧœáÂÛŁŹÊÔÓĂÒ»Ÿä»°±íÊöŁș______Łź
ĄŸŽđ°žĄżŁš1Ł©ąÙ![]() Ł»ąÚ
Ł»ąÚ![]() Ł»Łš2Ł©
Ł»Łš2Ł©![]() Ł»Łš3Ł©ąÙ”ă
Ł»Łš3Ł©ąÙ”ă![]() ÔÚÖ±Ïß
ÔÚÖ±Ïß![]() ÉÏŁŹŒŽ
ÉÏŁŹŒŽ![]() ŁŹ
ŁŹ![]() ŁŹ
ŁŹ![]() ÔÚÍŹÒ»ÌőÖ±ÏßÉÏŁ»ÀíÓÉŒûœâÎöŁ»ąÚ”ă
ÔÚÍŹÒ»ÌőÖ±ÏßÉÏŁ»ÀíÓÉŒûœâÎöŁ»ąÚ”ă![]() ¶ŒÔÚÍŹÒ»ÌőÏ߶Σš»òÖ±Ïߣ©ÉÏŁź
¶ŒÔÚÍŹÒ»ÌőÏ߶Σš»òÖ±Ïߣ©ÉÏŁź
ĄŸœâÎöĄż
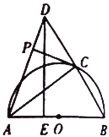
Łš1Ł©ąÙčę”ăE1ŚśE1NĄÍBCÓÚNŁŹœ»ADÓÚMŁŹÔòMNŁœABŁœ![]() ŁŹÓɔȱßÈęœÇĐΔÄĐÔÖÊ”ĂłöAP1ŁœAE1ŁœADŁœ8ŁŹAMŁœ4ŁŹE1MŁœ
ŁŹÓɔȱßÈęœÇĐΔÄĐÔÖÊ”ĂłöAP1ŁœAE1ŁœADŁœ8ŁŹAMŁœ4ŁŹE1MŁœ![]() ŁŹŒŽżÉ”ĂłöŽđ°žŁ»
ŁŹŒŽżÉ”ĂłöŽđ°žŁ»
ąÚŚśP2MĄÍADÓÚMŁŹÔòP2MĄÎABŁŹÉè”È±ßĄśAP2E2”ı߳€AE2ÎȘ2xŁŹÓɔȱßÈęœÇĐΔÄĐÔÖÊ”ĂłöAP2ŁœAE2Łœ2xŁŹAMŁœxŁŹP2MŁœ![]() ŁŹÓÉĄśP2MDĄŚĄśBADŁŹ”Ăłö
ŁŹÓÉĄśP2MDĄŚĄśBADŁŹ”Ăłö![]() ŁŹœű¶ű”ĂłöŽđ°žŁ»
ŁŹœű¶ű”ĂłöŽđ°žŁ»
Łš2Ł©čę![]() Śś
Śś![]() ÓÚ”ă
ÓÚ”ă![]() ŁŹŃÓł€
ŁŹŃÓł€![]() œ»
œ»![]() ÓÚ”ă
ÓÚ”ă![]() ŁŹÓɔȱßÈęœÇĐΔÄĐÔÖÊ”Ăłö
ŁŹÓɔȱßÈęœÇĐΔÄĐÔÖÊ”Ăłö![]() ŁŹ
ŁŹ![]() ŁŹÇółöHMŁœ
ŁŹÇółöHMŁœ![]() ADŁœ4ŁŹÓÉÆœĐĐÏß·ÖÏ߶γɱÈÀę”Ăłö
ADŁœ4ŁŹÓÉÆœĐĐÏß·ÖÏ߶γɱÈÀę”Ăłö![]() ŁŹŒŽżÉ”ĂłöŽđ°žŁ»
ŁŹŒŽżÉ”ĂłöŽđ°žŁ»
Łš3Ł©ÒÔBÎȘŚű±êԔ㣏ÒÔBCËùÔÚÖ±ÏßÎȘxÖᣏABËùÔÚÖ±ÏßÎȘyÖᣏœšÁąÆœĂæÖ±œÇŚű±êÏ”ŁŹÓÉŁš1Ł©Łš2Ł©”ĂŁș![]() ŁŹ
ŁŹ![]() ŁŹ
ŁŹ![]() ŁŹÓÉŽę¶šÏ”Êę·šÇółöčęE1ĄąE3”ÄÖ±ÏßœâÎöÊœŁŹŽúÈëE2œűĐĐŃéÖ€ŒŽżÉ”ĂłöœáÂÛŁ»
ŁŹÓÉŽę¶šÏ”Êę·šÇółöčęE1ĄąE3”ÄÖ±ÏßœâÎöÊœŁŹŽúÈëE2œűĐĐŃéÖ€ŒŽżÉ”ĂłöœáÂÛŁ»
ąÚÓÉąÙŒŽżÉ”ĂłöœáÂÛŁź
œâŁșŁš1Ł©ąÙĄßËıßĐÎABCDÊÇŸŰĐÎŁŹ
ĄàBCŁœADŁœ8ŁŹčę”ăE1ŚśE1NĄÍBCÓÚNŁŹœ»ADÓÚMŁŹÈçÍŒ1ËùÊŸŁș
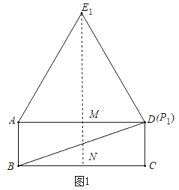
ÔòMNŁœABŁœ![]() ŁŹ
ŁŹ
ĄßËıßĐÎABCDÊÇŸŰĐÎŁŹ
ĄàADŁœBCŁœ8ŁŹ
ĄßĄśAP1E1ÊǔȱßÈęœÇĐÎŁŹ
ĄàAP1ŁœAE1ŁœADŁœ8ŁŹAMŁœ4ŁŹ
ĄàE1MŁœ![]() ŁŹ
ŁŹ
ĄàE1NŁœ![]() ŁŹŒŽ”ă
ŁŹŒŽ”ă![]() ”œ
”œ![]() ”ÄŸàÀëÊÇ
”ÄŸàÀëÊÇ![]() Ł»
Ł»
ąÚŚśP2MĄÍADÓÚMŁŹÈçÍŒ2ËùÊŸŁŹÔòP2MĄÎABŁŹ
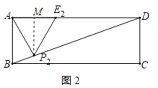
Éè”È±ßĄśAP2E2”ı߳€AE2Łœ2xŁŹ
ĄàAP2ŁœAE2Łœ2xŁŹAMŁœxŁŹP2MŁœ![]() ŁŹ
ŁŹ
ĄßP2MĄÎABŁŹ
ĄàĄśP2MDĄŚĄśBADŁŹ
Ąà![]() ŁŹŒŽ
ŁŹŒŽ![]() ŁŹ
ŁŹ
œâ”ĂŁșxŁœ![]() ŁŹ
ŁŹ
ĄàAE2Łœ2xŁœ![]() Ł»
Ł»
čÊŽđ°žÎȘŁș![]() Ł»
Ł»
Łš2Ł©čę![]() Śś
Śś![]() ÓÚ”ă
ÓÚ”ă![]() ŁŹŃÓł€
ŁŹŃÓł€![]() œ»
œ»![]() ÓÚ”ă
ÓÚ”ă![]() ŁŹ
ŁŹ
Ąß![]() ÊǔȱßÈęœÇĐÎŁŹ
ÊǔȱßÈęœÇĐÎŁŹ
Ąà![]() ŁŹ
ŁŹ![]() ŁŹ
ŁŹ
Ąà![]() ŁŹ
ŁŹ
Ąß![]() ŁŹ
ŁŹ
Ąà![]() ŁŹŒŽ
ŁŹŒŽ![]() ŁŹ
ŁŹ
Ąà![]() Ł»
Ł»
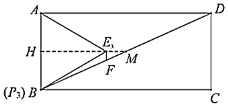
Łš3Ł©ąÙÒÔ![]() ÎȘŚű±êԔ㣏ÒÔ
ÎȘŚű±êԔ㣏ÒÔ![]() ËùÔÚÖ±ÏßÎȘ
ËùÔÚÖ±ÏßÎȘ![]() Öᣏ
Öᣏ![]() ËùÔÚÖ±ÏßÎȘ
ËùÔÚÖ±ÏßÎȘ![]() ÖᣏœšÁąÆœĂæÖ±œÇŚű±êÏ”ŁŹ
ÖᣏœšÁąÆœĂæÖ±œÇŚű±êÏ”ŁŹ
ÓÉŁš1Ł©ąÙąÚŁš2Ł©ËùÇóŁŹ”Ă![]() ŁŹ
ŁŹ![]() ŁŹ
ŁŹ![]() ŁŹ
ŁŹ
ÉèŸčę![]() ŁŹ
ŁŹ![]() ”ÄÖ±ÏßœâÎöÊœÎȘ
”ÄÖ±ÏßœâÎöÊœÎȘ![]()
![]() ŁŹ
ŁŹ
ÒÀÌâÒ⣏”Ă ŁŹœâ”Ă
ŁŹœâ”Ă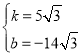 ŁŹ
ŁŹ
Ąà![]() ŁŹ
ŁŹ
°Ń![]() ŽúÈëÒ»ŽÎșŻÊęœâÎöÊœŁŹ”Ă
ŽúÈëÒ»ŽÎșŻÊęœâÎöÊœŁŹ”Ă![]() ŁŹ
ŁŹ
Ąà”ă![]() ÔÚÖ±Ïß
ÔÚÖ±Ïß![]() ÉÏŁŹŒŽ
ÉÏŁŹŒŽ![]() ŁŹ
ŁŹ![]() ŁŹ
ŁŹ![]() ÔÚÍŹÒ»ÌőÖ±ÏßÉÏŁ»
ÔÚÍŹÒ»ÌőÖ±ÏßÉÏŁ»
ąÚÓĂÒ»Ÿä»°±íÊöŁș”ă![]() ¶ŒÔÚÍŹÒ»ÌőÏ߶Σš»òÖ±Ïߣ©ÉÏŁź
¶ŒÔÚÍŹÒ»ÌőÏ߶Σš»òÖ±Ïߣ©ÉÏŁź