题目内容
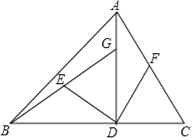
【题目】如图,AB是⊙O的直径,AC是⊙O的切线,BC交⊙O于点E,连接AE.
(1)若D为AC的中点,连接DE,证明:DE是⊙O的切线;
(2)若BE=3EC,求tan∠ABC.

【答案】见解析
【解析】试题分析:(1)要证明DE是⊙O的切线,只要证明![]() 等于90°即可,由题可得
等于90°即可,由题可得![]() =90°,从题上条件可得
=90°,从题上条件可得![]() ,
, ![]() ,所以可以得出
,所以可以得出![]() =90°,从而得出要求证结论。(2)BE=3EC,要想利用这个条件,可放在ECA和EAB中,证明ECAEAB,即可得到对应边成比例,进而得到AE、EC、EB三者之间的关系,再利用BE=3EC,求得tan∠ABC。
=90°,从而得出要求证结论。(2)BE=3EC,要想利用这个条件,可放在ECA和EAB中,证明ECAEAB,即可得到对应边成比例,进而得到AE、EC、EB三者之间的关系,再利用BE=3EC,求得tan∠ABC。
试题解析:证明:(1)连接OE,
∵AB是⊙O的直径,AC是圆⊙O的切线,
∴AE⊥BC,AC⊥AB,
在直角△AEC中,
∵D为AC的中点,
∴DE=DC,∴∠DEC=∠DCE,
∵∠OEB=∠OBE,∠ABC+∠ACB=90°,
∴∠DEC+∠OEB=∠DCE+∠OBE=90°,
∴∠DEO=180°﹣90°=90°,∴OE⊥DE,
∴DE 是⊙O的切线;
(2)在直角△EAC与直角△EBA中,
∵∠EAC+∠EAB=90°,∠EBA+∠EAB=90°,
∴∠EAC=∠EBA,
∴△EAC∽△EBA,
∴![]() ,EA2=EBEC
,EA2=EBEC
设EC=1,则EB=3,
EA2=EBEC=3, ![]() ,
,
在直角△AEB中, ![]() .
.

练习册系列答案
相关题目