题目内容
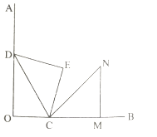
【题目】如图
，
是等腰直角三角形，点
、
分别在
、
上，
，将绕点顺时针旋转
，点
的对应点
恰好落在上，则
值为（）
A.
B.
C.
D.
【答案】B
【解析】
由等腰直角三角形的性质∠EDC=∠ECD=45°，从而CE=
CD，由旋转的性质得：∠MCN=∠DCE=∠ECD=45°，CM=CE=CD，∠DCN=75°，求出∠DCM=120°，得出∠OCD=60°，由锐角三角函数的知识求出OD=
CD，即可得出答案．
∵等腰三角形△CDE的顶点D、C在OA、OB上，∠M=90°，
∴∠EDC=∠ECD=45°，CE=CD，
由旋转的性质得：∠MCN=∠DCE=∠ECD=45°，CM=CE=CD，∠DCN=75°，
∴∠DCM=45°+75°=120°，
∴∠OCD=60°，
∴OD=sin60°×CD=CD,
∴
；
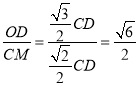故选B．
练习册系列答案
阅读快车系列答案
相关题目
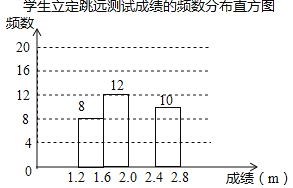
【题目】为了解某校九年级学生立定跳远水平，随机抽取该年级50名学生进行测试，并把测试成绩（单位：m）绘制成不完整的频数分布表和频数分布直方图．
学生立定跳远测试成绩的频数分布表
分组 | 频数 |
1.2≤x＜1.6 | a |
1.6≤x＜2.0 | 12 |
2.0≤x＜2.4 | b |
2.4≤x＜2.8 | 10 |
请根据图表中所提供的信息，完成下列问题：
（1）表中a= ，b= ，样本成绩的中位数落在 范围内；
（2）请把频数分布直方图补充完整；
（3）该校九年级共有1000名学生，估计该年级学生立定跳远成绩在2.4≤x＜2.8范围内的学生有多少人？
