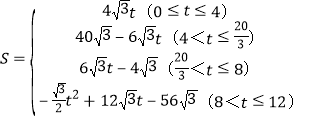��Ŀ����
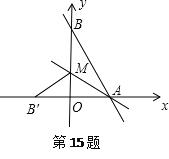
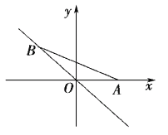
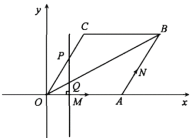
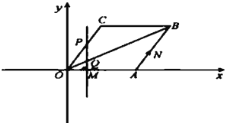
����Ŀ����ͼ����ֱ������ϵXOY�У�����OABC�ı�OA��x���������ϣ���B��C�ڵ�һ���ޣ���C=120�����߳�OA=8����M��ԭ��O������x����������ÿ��1����λ�����ٶ��������˶�����N��A�����ر�AB��BC��CO��ÿ��2����λ�����ٶ��������˶�.����M��ֱ��MP��ֱ��x�Ტ������OCB��P�����Խ���OB��Q����M�͵�Nͬʱ�������ֱ��ظ���·���˶�����N�˶���ԭ��Oʱ��M��N����ͬʱֹͣ�˶�.
��1����t=2ʱ�����߶�PQ�ij���
��2����tΪ��ֵʱ����P��N�غϣ�
��3�����APN�����ΪS����S��t�ĺ�����ϵʽ��t��ȡֵ��Χ.
���𰸡���1��PQ=![]() ����2��t=
����2��t=![]() ��ʱ����P��N�غ�����3��S��t�ĺ�����ϵʽΪ��
��ʱ����P��N�غ�����3��S��t�ĺ�����ϵʽΪ��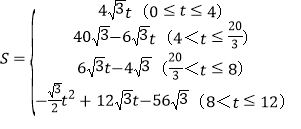 .
.
����������1����ֱ�����������PM��QM���ɽ�����⣻
��2�����ݵ�P��N��·��֮��=24���������̼��ɽ��������
��3�����������ο������⼴�ɽ������.
��1��������OABC����AOC=60������AOQ=30����
��t=2ʱ��OM=2��PM=2![]() ��QM=
��QM=![]() ��PQ=
��PQ=![]() .
.
��2����t��4ʱ��AN=PO=2OM=2t��
t=4ʱ��P����C�㣬N����B�㣬��P��N�ڱ�BC������.
��t��ʱ����P��N�غϣ���(t-4)+2(t-4)=8,
��t=![]() .
.
��t=![]() ��ʱ����P��N�غ�.
��ʱ����P��N�غ�.
��3���ٵ�0��t��4ʱ��PN=OA=8����PN��OA��PM=![]() t��
t��
S��APN=![]() ��8��
��8��![]() t=4
t=4![]() t��
t��
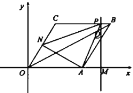
�ڵ�4��t��![]() ʱ��PN=8-3(t-4)=20-3t��
ʱ��PN=8-3(t-4)=20-3t��
S��APN=![]() ��4
��4![]() ��(20-3t)=40
��(20-3t)=40![]() -6
-6![]() t��
t��
�۵�![]() ��t��8ʱ��PN=3(t-4)-8=3t-20��
��t��8ʱ��PN=3(t-4)-8=3t-20��
S��APN=![]() ��4
��4![]() ��(3t-20)= 6
��(3t-20)= 6![]() t -4
t -4![]() ��
��
��8��t��12ʱ��ON=24-2t��N��OM����Ϊ12![]() -
-![]() t,
t,
N��CP����Ϊ4![]() -(12
-(12![]() -
-![]() t)=
t)= ![]() t-8
t-8![]() ��CP=t-4��BP=12-t��
��CP=t-4��BP=12-t��
S��APN=S����-S��AON- S��CPN- S��APB
=32![]() -
-![]() ��8��(12
��8��(12![]() -
-![]() t)-
t)- ![]() ��t-4����
��t-4����![]() t-8
t-8![]() ��-
��-![]() ��12-t����4
��12-t����4![]()
= - ![]() t2+12
t2+12![]() t-56
t-56![]()
���ϣ�S��t�ĺ�����ϵʽΪ��