题目内容
【题目】如图,在平面直角坐标系中,等边三角形△ABO的边长为4.
(1)求点A的坐标.
(2)若点P从点O出发以每秒1个单位的速度沿x轴正方向运动,运动时间为t秒,△PAB的面积为S,求S与t的关系式,并直接写出t的范围.
(3)在(2)的条件下,当点P在点B的右侧时,若S=![]() ,在平面内是否存在点Q,使点P、Q、A、B围成的四边形是平行四边形?若存在,求出点Q坐标;若不存在,请说明理由.
,在平面内是否存在点Q,使点P、Q、A、B围成的四边形是平行四边形?若存在,求出点Q坐标;若不存在,请说明理由.
【答案】(1)A(2,2![]() );(2)当0≤t<4时,S=-
);(2)当0≤t<4时,S=-![]() t+4
t+4![]() ;当t>4时,S=
;当t>4时,S=![]() t﹣4
t﹣4![]() ;(3)存在, Q的坐标为(3,2
;(3)存在, Q的坐标为(3,2![]() )或(1,2
)或(1,2![]() )或(7,﹣2
)或(7,﹣2![]() )
)
【解析】
(1)利用等边三角形的性质即可得出结论;
(2)分点P在边OB和OB的延长线上,利用三角形的面积公式即可得出结论;
(3)分三种情况,利用中点坐标公式和平行四边形的对角线互相平分,建立方程求解即可得出结论.
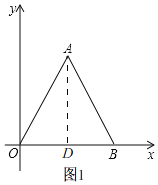
解:(1)如图1,过点A作AD⊥x轴于D,
∵△ABC是等边三角形,
∴∠AOD=60°,OD=![]() OB=2,
OB=2,
在Rt△AOD中,AD=![]() OD=2
OD=2![]() ,
,
∴A(2,2![]() );
);
(2)由运动知,OP=t,
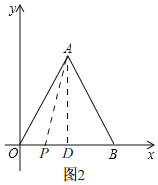
当0≤t<4时,如图2,BP=OB﹣OP=4﹣t,
∴S=S△ABP=![]() BPAD=
BPAD=![]() (4﹣t)×2
(4﹣t)×2![]() =﹣
=﹣![]() t+4
t+4![]() ,
,
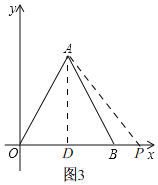
当t>4时,如图3,BP=OP﹣OB=t﹣4,
∴S=S△ABP=![]() BPAD4=
BPAD4=![]() (t﹣4
(t﹣4![]() =
=![]() t﹣4
t﹣4![]() ;
;
(3)由(2)知,点P在点B右侧时,t>4,S=![]() t﹣4
t﹣4![]() ,
,
∵S=![]() ,
,
∴![]() t﹣4
t﹣4![]() =
=![]() ,
,
∴t=5,
∴P(5,0),
∵等边△ABC的边长为4,
∴B(4,0),
∵A(2,2![]() ),设Q(m,n),
),设Q(m,n),
∵使点P、Q、A、B围成的四边形是平行四边形,
∴①当AP为对角线时,
∴AP与BQ互相平分,
∴![]() (2+5)=
(2+5)=![]() (4+m),
(4+m),![]() (2
(2![]() +0)=
+0)=![]() (0+n),
(0+n),
∴m=3,n=2![]() ,
,
∴Q(3,2![]() ),
),
②当AB为对角线时,∴AB与PQ互相平分,
∴![]() (2+4)=
(2+4)=![]() (5+m),
(5+m),![]() (2
(2![]() +0)=
+0)=![]() (0+n),
(0+n),
∴m=1,n=2![]() ,
,
∴Q(1,2![]() ),
),
③当BP为对角线时,∴BP与AQ互相平分,
∴![]() (4+5)=
(4+5)=![]() (2+m),
(2+m),![]() (0+0)=
(0+0)=![]() (2
(2![]() +n),
+n),
∴m=7,n=﹣2![]() ,
,
∴Q(7,﹣2![]() ),
),
即:满足条件的点Q的坐标为(3,2![]() )或(1,2
)或(1,2![]() )或(7,﹣2
)或(7,﹣2![]() ).
).
故答案为:(1)A(2,2![]() );(2)当0≤t<4时,S=-
);(2)当0≤t<4时,S=-![]() t+4
t+4![]() ;当t>4时,S=
;当t>4时,S=![]() t﹣4
t﹣4![]() ;(3)存在, Q的坐标为(3,2
;(3)存在, Q的坐标为(3,2![]() )或(1,2
)或(1,2![]() )或(7,﹣2
)或(7,﹣2![]() ).
).

 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案