题目内容
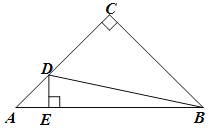
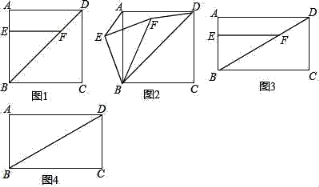
【题目】在四边形ABCD中，点E为AB边上的一点，点F为对角线BD上的一点，且EF⊥AB．
（1）若四边形ABCD为正方形．
①如图1，请直接写出AE与DF的数量关系 ；
②将△EBF绕点B逆时针旋转到图2所示的位置，连接AE，DF，猜想AE与DF的数量关系并说明理由．
（2）若四边形ABCD为矩形，BC=mAB，其他条件都不变．
①如图3，猜想AE与DF的数量关系并说明理由；
②将△EBF绕点B顺时针旋转α（0°＜α＜90°）得到△E′BF′，连接AE′，DF′，请在图4中画出草图，并直接写出AE′和DF′的数量关系．
【答案】（1)DF=
AE；DF=AE；（2）DF=
MF=AE；DF′=AE′.
【解析】
（1）①利用正方形的性质得△ABD为等腰直角三角形，则BD=AB，再证明△BEF为等腰直角三角形得到BF=BE，所以BD-BF=AB-BE，从而得到DF=AE；
②利用旋转的性质得∠ABE=∠DBF，结合
=, 则根据相似三角形的判定可得到△ABE∽△DBF，所以
=;
（2）①作FM⊥AD，垂足为M．依据勾股定理可得Rt△ABD中，BD=
=AB，再根据△DMF∽△ABD，可得
=,即可得出DF=AE；
②依据△BEF∽△BAD，可得=,进而得出
=,即可得出△ABE′∽△DBF′，进而得到
=,即DF′=AE′．
解：（1）①∵四边形ABCD为正方形，
∴△ABD为等腰直角三角形，
∴BD=AB，
∵EF⊥AB，
∴△BEF为等腰直角三角形，
BF=BE，
∴BD﹣BF=AB﹣BE，
即DF=AE，
故答案为：DF=AE；
②DF=AE．理由如下：
∵△EBF绕点B逆时针旋转到图2所示的位置，
∴∠ABE=∠DBF，
∵
= ，
=，
∴，
∴△ABE∽△DBF，
∴=，
即AE与DF的数量关系是：DF=AE；
（2）①AE与DF的数量关系是：DF=AE；
理由：在图3中，作FM⊥AD，垂足为M．
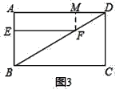
∵∠A=∠AEF=∠AMF=90°，
∴四边形AEFM是矩形，
∴FM=AE，
∵AD=BC=mAB，
∴Rt△ABD中，BD==AB，
∵MF∥AB，
∴△DMF∽△ABD，
∴=，
∴DF=MF=AE；
②AE′和DF′的数量关系：DF'=AE'．
如图3，∵四边形ABCD为矩形，
∴AD=BC=mAB，
∴BD==AB，
∵EF⊥AB，
∴EF∥AD，
∴△BEF∽△BAD，
∴
，
∴
=，
如图4，∵△EBF绕点B顺时针旋转α（0°＜α＜90°）得到△E'BF'，
∴∠ABE′=∠DBF′，BE′=BE，BF′=BF，
∴=，
∴△ABE′∽△DBF′，
∴=，
即DF′=AE′．
