题目内容
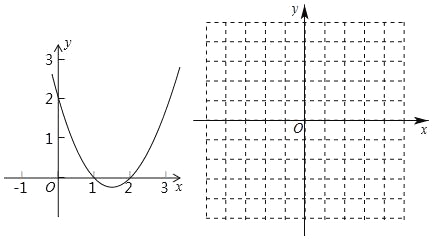
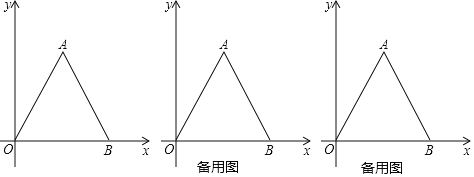
【题目】如图1,在边长为3的等边![]() 中,点
中,点![]() 从点
从点![]() 出发沿射线
出发沿射线![]() 方向运动,速度为1个单位/秒,同时点
方向运动,速度为1个单位/秒,同时点![]() 从点
从点![]() 出发,以相同的速度沿射线
出发,以相同的速度沿射线![]() 方向运动,过点
方向运动,过点![]() 作
作![]() 交射线
交射线![]() 于点
于点![]() ,连接
,连接![]() 交射线
交射线![]() 于点
于点![]() .
.
(1)如图1,当![]() 时,求运动了多长时间?
时,求运动了多长时间?
(2)如图1,当点![]() 在线段
在线段![]() (不考虑端点)上运动时,是否始终有
(不考虑端点)上运动时,是否始终有![]() ?请说明理由;
?请说明理由;
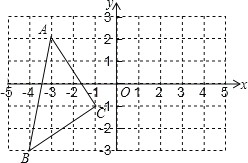
(3)如图2,过点![]() 作
作![]() ,垂足为
,垂足为![]() ,当点
,当点![]() 在线段
在线段![]() (不考虑端点)上时,
(不考虑端点)上时,![]() 的长始终等于
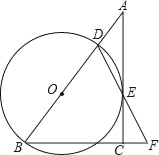
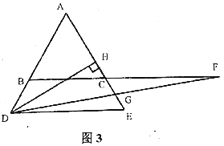
的长始终等于![]() 的一半;如图3,当点
的一半;如图3,当点![]() 运动到
运动到![]() 的延长线上时,
的延长线上时,![]() 的长是否发生变化?若改变,请说明理由;若不变,求出
的长是否发生变化?若改变,请说明理由;若不变,求出![]() 的长.
的长.
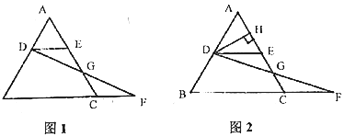
【答案】(1)运动了1秒;(2)始终有![]() ,证明见解析;(3)不变,
,证明见解析;(3)不变,![]() .
.
【解析】
(1)设运动了![]() 秒,则
秒,则![]() ,
,![]() ,
,![]() ,根据
,根据![]() 列方程求解即可;
列方程求解即可;
(2)先证明DE=CF,然后根据“ASA”证明![]() ,从而可证始终有
,从而可证始终有![]() ;
;
(3)根据DE//BC得出∠ADE=∠B=60°,然后再在利用等边三角形的性质得出![]() ,再证明
,再证明![]() ,得到
,得到![]() ,根据
,根据![]() 可解.
可解.
解:(1)设运动了![]() 秒,则
秒,则![]() ,
,![]() ,
,![]() ,
,
当![]() 时,
时,
∵![]() ,
,
∴![]() ,
,
∴![]() ,即
,即![]() ,
,
解得![]() ,
,
∴运动了1秒.
(2)∵![]() ,
,
∴![]() ,
,
∴![]() 是等边三角形,
是等边三角形,
∴![]()
∵![]()
∴![]()
又∵![]()
∴![]() ,
,![]() .
.
在![]() 与
与![]() 中
中
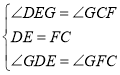
∴![]()
∴![]() ;
;
(3)不变.
理由:∵![]() ,
,
∴![]() ,
,
∴![]() 是等边三角形,
是等边三角形,
∵![]() ,
,
∴![]() ,
,
在![]() 与
与![]() 中
中
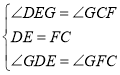 ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() .
.

练习册系列答案
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案
相关题目