题目内容
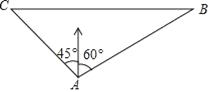
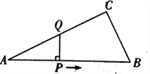
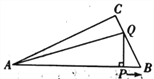
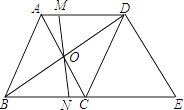
【题目】如图,在△ABC中,BC=AC=4,∠ACB =90°,点M是边AC的中点,点P是边AB上
的动点,则PM+PC的最小值为_______.
【答案】![]()
【解析】试题分析:作点C关于AB的对称点C′,连接C′M与AB交于点P,连接PM、PC.此时PM+PC= C′M最小,在Rt△BM C′中利用勾股定理即可求出最小值.
解:作点C关于AB的对称点C′交AB于点O,连接C′M与AB交于点P,连接PM、PC、C′B ,此时PM+PC= C′M最小.
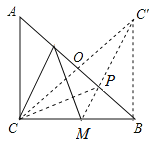
由对称性可知∠C′BP=∠CBP=45°,
∴∠CBC′=90°,
∴BC′⊥BC,∠BCC′=∠BC′C=45°,
∴BC′=BC=4,
∵M是BC边的中点,
∴BM=2,
根据勾股定理可得:MC′=![]()
所以PM+PC的最小值是![]() .
.
故答案为: ![]()

练习册系列答案
相关题目
【题目】根据下列表格的对应值,判断方程ax2+bx+c=0(a≠0,a,b,c为常数)一个解的范围是( )
x | 3.23 | 3.24 | 3.25 | 3.26 |
ax2+bx+c | -0.06 | -0.02 | 0.03 | 0.09 |
A. 3<x<3.23 B. 3.23<x<3.24
C. 3.24<x<3.25 D. 3.25<x<3.26