题目内容
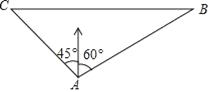
【题目】一艘轮船在小岛A的北偏东60°距小岛80海里的B处,沿正西方向航行2小时后到达小岛的北偏西45°的C处,则该船行驶的速度为_____海里/小时.
【答案】20+20![]()
【解析】试题分析:设该船行驶的速度为x海里/时,由已知可得BC=3x,AQ⊥BC,∠BAQ=60°,∠CAQ=45°,AB=80海里,在直角三角形ABQ中求出AQ、BQ,再在直角三角形AQC中求出CQ,得出BC=40+40![]() =2x,解方程即可.
=2x,解方程即可.
解:如图所示:
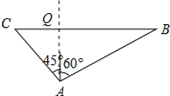
设该船行驶的速度为x海里/时,
3小时后到达小岛的北偏西45°的C处,
由题意得:AB=80海里,BC=2x海里,
在直角三角形ABQ中,∠BAQ=60°,
∴∠B=90°﹣60°=30°,
∴AQ=![]() AB=40,BQ=
AB=40,BQ=![]() AQ=40
AQ=40![]() ,
,
在直角三角形AQC中,∠CAQ=45°,
∴CQ=AQ=40,
∴BC=40+40![]() =3=2x,
=3=2x,
解得:x=20+20![]() .
.
即该船行驶的速度为20+20![]() 海里/时;
海里/时;
故答案为:20+20![]() .
.

练习册系列答案
 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案
相关题目
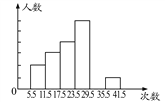
【题目】为了进一步了解九年级500名学生的身体素质情况,体育老师对九年级(1)班50名学生进行一分钟跳绳次数测试,以测试数据为样本,绘制出部分频数分布表和部分频数分布直方图如下所示: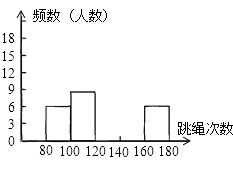
组别 | 次数x | 频数(人数) |
第l组 | 80≤x<100 | 6 |
第2组 | 100≤x<120 | 8 |
第3组 | 120≤x<140 | a |
第4组 | 140≤x<160 | 18 |
第5组 | 160≤x<180 | 6 |
请结合图表完成下列问题:
(1)表中的a=,次数在140≤x<160这组的频率为;
(2)请把频数分布直方图补充完整;
(3)若九年级学生一分钟跳绳次数(x)达标要求是:x<120不合格;x≥120为合格,则这个年级合格的学生有人.