Question

【题目】如图，在菱形ABCD中，对角线AC与BD相交于点O，MN过点O且与边AD、BC分别交于点M和点N．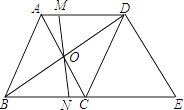

（1）请你判断OM与ON的数量关系，并说明理由；
（2）过点D作DE∥AC交BC的延长线于E，当AB=5，AC=6时，求△BDE的周长．

Answer 1

【答案】
（1）解：∵四边形ABCD是菱形，

∴AD∥BC，AO=OC，

∴ = =1，

∴OM=ON

（2）解：∵四边形ABCD是菱形，

∴AC⊥BD，AD=BC=AB=5，

∴BO= =4，

∴BD=2BO=8，

∵DE∥AC，AD∥CE，

∴四边形ACED是平行四边形，

∴DE=AC=6，

∴△BDE的周长是：

BD+DE+BE

=BD+AC+（BC+CE）

=8+6+（5+5）

=24

即△BDE的周长是24．

【解析】（1）根据菱形的性质，得到对边平行对角线互相平分，得出比例，得到OM=ON；（2）根据菱形的性质，对角线互相垂直平分，再根据勾股定理求出BO的值，得到四边形ACED是平行四边形，求出△BDE的周长即可.
【考点精析】掌握菱形的性质是解答本题的根本，需要知道菱形的四条边都相等；菱形的对角线互相垂直，并且每一条对角线平分一组对角；菱形被两条对角线分成四个全等的直角三角形；菱形的面积等于两条对角线长的积的一半．