题目内容
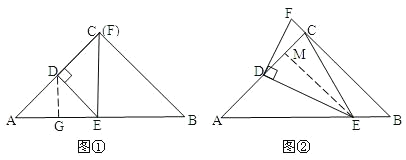
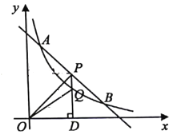
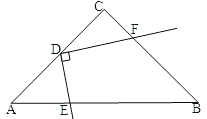
【题目】如图,在Rt△ABC中,∠C=90°,AC=BC=6,点D为AC中点,点E为边AB上一动点,点F为射线BC上一动点,且∠FDE=90°.
(1)当DF∥AB时,连接EF,求∠DEF的余切值;
(2)当点F在线段BC上时,设AE=x,BF=y,求y关于x的函数关系式,并写出x的取值范围;
(3)连接CE,若△CDE为等腰三角形,求BF的长.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)6或7
;(3)6或7
【解析】
(1)先根据勾股定理求出AB的长,再由三角形的中位线定理求出DF的长,利用等腰直角三角形的性质求出DE的长,由锐角三角函数的定义即可求出∠DEF的余切值;
(2)过点E作EH⊥AC于点H,由平行线的性质及等腰三角形的性质可求出HE、HD的表达式,再由相似三角形的判定定理求出△HDE∽△CFD,根据相似三角形的性质可写出y关于x的函数关系式;
(3)先分析出△DCE为等腰三角形时的两种情况,再根据题意画出图形,当DC=DE时,证明∠AEC=90°,得到AE=CE,再根据等腰三角形三线合一得到DE⊥AC,从而得到F与C重合,进而得出BF的长;当ED=EC时,先判断出点F的位置,再根据相似三角形的性质及判定定理即可解答.
(1)∵AC=BC=6,∠ACB=90°,
∴∠A=∠B=45°,![]() .
.
∵DF∥AB,![]() ,
,
∴∠AED=∠EDF=90°,![]() ,
,
∴△ADE是等腰直角三角形,
∴![]() .
.
在Rt△DEF中,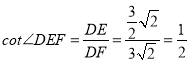 ;
;
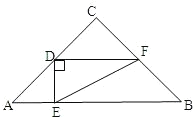
(2)过点E作EH⊥AC于点H.
∵BC⊥AC,
∴EH∥BC,
∴∠AEH=∠B.
∵∠B=∠A,
∴∠AEH=∠A,![]() ,
,
∴![]() .
.
∵∠EDF=90°,
∴∠EDH+∠CDF=90°.
∵∠C=90°,
∴∠CDF+∠CFD=90°,
∴∠EDH=∠CFD.
∵∠EHD=∠C=90°,
∴△HDE∽△CFD,
∴![]() ,
,
∴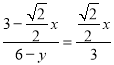 ,
,
∴![]() ;
;
(3)∵![]() ,CD=3,
,CD=3,
∴CE>CD,
∴若△DCE为等腰三角形,只有DC=DE或ED=EC两种可能.
①当DC=DE时,(如图①)
∵DC=DE,
∴∠DCE=∠DEC.
∵AD=CD,DE=DC,
∴AD=DE,
∴∠A=∠AED.
∵∠A+∠AED+∠DEC+∠DCE=180°,
∴∠AED+∠DEC=90°,
∴∠AEC=90°,
∴CE⊥AB.
∵AC=BC,
∴AE=![]() AB=
AB=![]() ,
,
∵∠A=45°,∠AEC=90°,
∴AE=CE.
∵AD=CD,
∴DE⊥AC,
∴此时F与C重合,
∴BF=6;
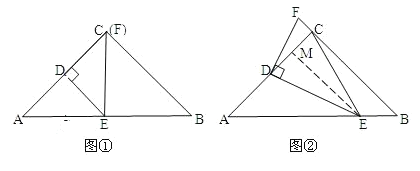
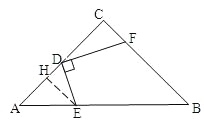
②当ED=EC时,点F在BC的延长线上,
过点E作EM⊥CD于点M,(如图②)
∵ED=EC,EM⊥CD,
∴DM=![]() CD=
CD=![]() .
.
∵EM⊥CD,
∴△DME是直角三角形.
∵DE⊥DF,
∴∠EDM+∠FDC=90°.
∵∠FDC+∠F=90°,
∴∠F=∠EDM,
∴△DFC∽△EDM,
∴![]() ,
,
∴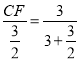 ,
,
∴CF=1,
∴BF=7,
综上所述:BF为6或7.