题目内容
(2013•牡丹江)博雅书店准备购进甲、乙两种图书共100本,购书款不高于2224元,预计这100本图书全部售完的利润不低于1100元,两种图书的进价、售价如下表所示:
请解答下列问题:
(1)有哪几种进书方案?
(2)在这批图书全部售出的条件下,(1)中的哪种方案利润最大?最大利润是多少?
(3)博雅书店计划用(2)中的最大利润购买单价分别为72元、96元的排球、篮球捐给贫困山区的学校,那么在钱恰好用尽的情况下,最多可以购买排球和篮球共多少个?请你直接写出答案.
| 甲种图书 | 乙种图书 | |
| 进价(元/本) | 16 | 28 |
| 售价(元/本) | 26 | 40 |
(1)有哪几种进书方案?
(2)在这批图书全部售出的条件下,(1)中的哪种方案利润最大?最大利润是多少?
(3)博雅书店计划用(2)中的最大利润购买单价分别为72元、96元的排球、篮球捐给贫困山区的学校,那么在钱恰好用尽的情况下,最多可以购买排球和篮球共多少个?请你直接写出答案.
分析:(1)利用购书款不高于2224元,预计这100本图书全部售完的利润不低于1100元,结合表格中数据得出不等式组,求出即可;
(2)根据乙种书利润较高,故乙种书购进越多利润最大,故购进甲种书:48种,乙种书:52本利润最大求出即可;
(3)根据题意得出:72a+96b=1104,尽可能多买排球才能购买数量最多,故当买一个篮球时,求出可以购买排球个数,正好是整数.
(2)根据乙种书利润较高,故乙种书购进越多利润最大,故购进甲种书:48种,乙种书:52本利润最大求出即可;
(3)根据题意得出:72a+96b=1104,尽可能多买排球才能购买数量最多,故当买一个篮球时,求出可以购买排球个数,正好是整数.
解答:解:(1)设购进甲种图书x本,则购进乙书(100-x)本,根据题意得出:
,
解得:48≤x≤50.
故有3种购书方案:甲种书:48本,乙种书:52本;甲种书:49本,乙种书:51本;甲种书:50本,乙种书:50本;
(2)根据乙种书利润较高,故乙种书购进越多利润最大,
故购进甲种书:48种,乙种书:52本利润最大为:48×(26-16)+52×(40-28)=1104(元);
(3)设购买a个排球,b个篮球.
根据题意得出:72a+96b=1104,
尽可能多买排球才能购买数量最多,故当买一个篮球时,可以购买:(1104-96)÷72=14(个).
答:最多可以购买排球和篮球共15个.
|
解得:48≤x≤50.
故有3种购书方案:甲种书:48本,乙种书:52本;甲种书:49本,乙种书:51本;甲种书:50本,乙种书:50本;
(2)根据乙种书利润较高,故乙种书购进越多利润最大,
故购进甲种书:48种,乙种书:52本利润最大为:48×(26-16)+52×(40-28)=1104(元);
(3)设购买a个排球,b个篮球.
根据题意得出:72a+96b=1104,
尽可能多买排球才能购买数量最多,故当买一个篮球时,可以购买:(1104-96)÷72=14(个).
答:最多可以购买排球和篮球共15个.
点评:此题主要考查了不等式组的应用以及二元一次方程的应用以及最佳方案问题,正确得出不等式关系是解题关键.

练习册系列答案
相关题目
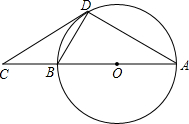 (2013•牡丹江)如图,点C是⊙O的直径AB延长线上的一点,且有BO=BD=BC.
(2013•牡丹江)如图,点C是⊙O的直径AB延长线上的一点,且有BO=BD=BC.