题目内容
(2013•牡丹江)在平面直角坐标系中,点O是坐标原点,过点A(1,2)的直线y=kx+b与x轴交于点B,且S△AOB=4,则k的值是
k=
或-
| 2 |
| 5 |
| 2 |
| 3 |
k=
或-
.| 2 |
| 5 |
| 2 |
| 3 |
分析:先表示出B点坐标为(-
,0);再把A(1,2)代入y=kx+b得k+b=2,则b=2-k,然后根据三角形面积公式得到
|-
|•2=4,即|
|=4,所以|
|=4,然后解方程即可.
| b |
| k |
| 1 |
| 2 |
| b |
| k |
| b |
| k |
| 2-k |
| k |
解答:解:把y=0代入y=kx+b得kx+b=0,解得x=-
,所以B点坐标为(-
,0);
把A(1,2)代入y=kx+b得k+b=2,则b=2-k,
∵S△AOB=4,
∴
|-
|•2=4,即|
|=4,
∴|
|=4,
解得k=
或-
.
故答案为k=
或-
.
| b |
| k |
| b |
| k |
把A(1,2)代入y=kx+b得k+b=2,则b=2-k,
∵S△AOB=4,
∴
| 1 |
| 2 |
| b |
| k |
| b |
| k |
∴|
| 2-k |
| k |
解得k=
| 2 |
| 5 |
| 2 |
| 3 |
故答案为k=
| 2 |
| 5 |
| 2 |
| 3 |
点评:本题考查了一次函数图象上点的坐标特征:一次函数y=kx+b(k≠0)的图象上的点满足其解析式.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
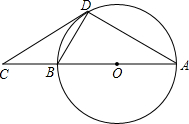 (2013•牡丹江)如图,点C是⊙O的直径AB延长线上的一点,且有BO=BD=BC.
(2013•牡丹江)如图,点C是⊙O的直径AB延长线上的一点,且有BO=BD=BC.