题目内容
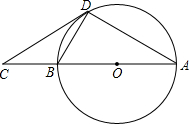 (2013•牡丹江)如图,点C是⊙O的直径AB延长线上的一点,且有BO=BD=BC.
(2013•牡丹江)如图,点C是⊙O的直径AB延长线上的一点,且有BO=BD=BC.(1)求证:CD是⊙O的切线;
(2)若半径OB=2,求AD的长.
分析:(1)由于BO=BD=BC,即DB为△ODC的边OC的中线,且有DB=
OC,则∠ODC=90°,然后根据切线的判定方法即可得到结论;
(2)由AB为⊙O的直径得∠BDA=90°,而BO=BD=2,则AB=2BD=4,然后根据勾股定理可计算出AD.
| 1 |
| 2 |
(2)由AB为⊙O的直径得∠BDA=90°,而BO=BD=2,则AB=2BD=4,然后根据勾股定理可计算出AD.
解答:(1)证明:连结OD,如图,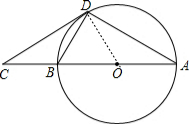
∵BO=BD=BC,
∴BD为△ODC的中线,且DB=
OC,
∴∠ODC=90°,
∴OD⊥CD,
而OD为⊙O的半径,
∴CD是⊙O的切线;
(2)解:∵AB为⊙O的直径,
∴∠BDA=90°,
∵BO=BD=2,
∴AB=2BD=4,
∴AD=
=2
.

∵BO=BD=BC,
∴BD为△ODC的中线,且DB=
| 1 |
| 2 |
∴∠ODC=90°,
∴OD⊥CD,
而OD为⊙O的半径,
∴CD是⊙O的切线;
(2)解:∵AB为⊙O的直径,
∴∠BDA=90°,
∵BO=BD=2,
∴AB=2BD=4,
∴AD=
| AB2-BD2 |
| 3 |
点评:本题考查了切线的判定定理:过半径的外端点且与半径垂直的直线为圆的切线.也考查了直角三角形的判定方法、勾股定理.

练习册系列答案
相关题目
