题目内容
已知抛物线y=ax2+3x+(a-2),a是常数且a<0,下列选项中可能是它大致图象的是( )
A、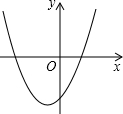 | B、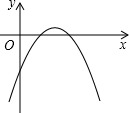 | C、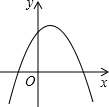 | D、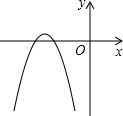 |
练习册系列答案
 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案
相关题目
我们学习了一次函数、二次函数和反比例函数,回顾学习过程,都是按照列表、描点、连线得到函数的图象,然后根据函数的图象研究函数的性质,这种研究方法主要体现的数学思想是( )
| A、演绎 | B、数形结合 | C、抽象 | D、公理化 |
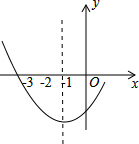 如图是二次函数y=ax2+bx+c图象的一部分,其对称轴为x=-1,且过点(-3,0).下列说法:①abc<0;②2a-b=0;③4a+2b+c<0;④3a+c=0;其中说法正确的是( )
如图是二次函数y=ax2+bx+c图象的一部分,其对称轴为x=-1,且过点(-3,0).下列说法:①abc<0;②2a-b=0;③4a+2b+c<0;④3a+c=0;其中说法正确的是( )| A、①② | B、②③ | C、①②④ | D、②③④ |
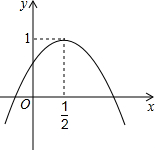 如图,二次函数y=ax2+bx+c的图象与y轴正半轴相交,其顶点坐标为(
如图,二次函数y=ax2+bx+c的图象与y轴正半轴相交,其顶点坐标为(| 1 |
| 2 |
| A、4 | B、3 | C、2 | D、1 |
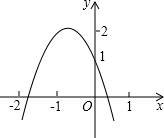 如图所示,二次函数y=ax2+bx+c(a≠0)的图象经过点(-1,2),且与x轴交点的横坐标为x1、x2,其中-2<x1<-1、0<x2<1.下列结论:
如图所示,二次函数y=ax2+bx+c(a≠0)的图象经过点(-1,2),且与x轴交点的横坐标为x1、x2,其中-2<x1<-1、0<x2<1.下列结论:①4a-2b+c<0,②2a-b<0,③a<-1,④b2+8a>4ac,⑤abc<0,
正确的结论是( )
| A、2个 | B、3个 | C、4个 | D、5个 |
抛物线y=x2-3x+2与y轴交点的坐标是( )
| A、(0,0) | B、(2,0) | C、(0,2) | D、(0,-1) |
若关于x的一元二次方程x2+ax+b=0有两个不同的实数根m,n(m<n),方程x2+ax+b=1有两个不同的实数p,q(p<q),则m,n,p,q的大小关系为( )
| A、m<p<q<n | B、p<m<n<q | C、m<p<n<q | D、p<m<q<n |

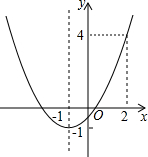 已知二次函数y=ax2+bx+c(a≠0)的图象如图,有下列结论:
已知二次函数y=ax2+bx+c(a≠0)的图象如图,有下列结论: