题目内容

若关于x的一元二次方程x2+ax+b=0有两个不同的实数根m，n（m＜n），方程x2+ax+b=1有两个不同的实数p，q（p＜q），则m，n，p，q的大小关系为（　　）
A、m＜p＜q＜nB、p＜m＜n＜qC、m＜p＜n＜qD、p＜m＜q＜n
练习册系列答案
相关题目
已知抛物线y=ax2+3x+（a-2），a是常数且a＜0，下列选项中可能是它大致图象的是（　　）
A、B、C、D、
在平面直角坐标系中，函数y=x2-2x（x≥0）的图象为C1，C1关于原点对称的图象为C2，则直线y=a（a为常数）与C1、C2的交点共有（　　）
A、1个B、1个或2个C、1个或2个或3个D、1个或2个或3个或4个
将二次函数y=x2-2x-1的图象绕坐标原点O旋转180°，则旋转后的图象对应的解析式为（　　）
A、y=x2+2x+3B、y=-x2-2x+1C、y=x2-2x-1D、y=-x2+2x-3
二次函数y=（x-2）2+1的最小值是（　　）
A、-1B、1C、2D、-2
已知抛物线y=ax2+bx+c与x轴的两个公共点之间的距离为1．若将抛物线y=ax2+bx+c向上平移一个单位，则它与x轴只有一个公共点；若将抛物线y=ax2+bx+c向下平移一个单位，则它经过原点，则抛物线y=ax2+bx+c为（　　）
A、y=4x2+4
2
x+1
B、y=4x2+4
2
x+1或y=4x2-4
2
x+1
C、y=4x2+4
2
x-1
D、y=4x2+4
2
x-1或y=4x2-4
2
x-1
二次函数y=x2+bx的图象如图，对称轴为直线x=1，若关于x的一元二次方程x2+bx-t=0（t为实数）在-1＜x＜4的范围内有解，则t的取值范围是（　　）
A、t≥-1B、-1≤t＜3C、-1≤t＜8D、3＜t＜8
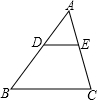如图，在△ABC中，点D，E分别在边AB，AC上，DE∥BC，已知AE=6，
AD
AB
=
3
7
，则EC的长是（　　）
A、4.5B、8
C、10.5D、14
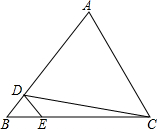如图，在△ABC中，D、E分别是AB、BC上的点，且DE∥AC，若S△BDE：S△CDE=1：4，则S△BDE：S△ACD=（　　）
A、1：16B、1：18C、1：20D、1：24

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网