题目内容
(本题10分)
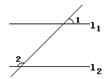
如图1,MA1∥NA2,则∠A1+∠A2=______________________度。
如图2,MA1∥NA3,则∠A1+∠A2+∠A3=________________________度。
如图3,MA1∥NA4,则∠A1+∠A2+∠A3+∠A4=__________________度。
如图4,MA1∥NA5,则∠A1+∠A2+∠A3+∠A4+∠A5=_____________________度。从上述结论中你发现了什么规律?
如图5,MA1∥NAn,则∠A1+∠A2+∠A3+……+∠An=______________________度。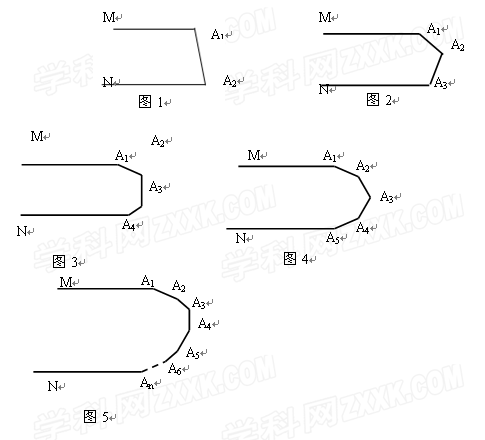
如图1,MA1∥NA2,则∠A1+∠A2=______________________度。
如图2,MA1∥NA3,则∠A1+∠A2+∠A3=________________________度。
如图3,MA1∥NA4,则∠A1+∠A2+∠A3+∠A4=__________________度。
如图4,MA1∥NA5,则∠A1+∠A2+∠A3+∠A4+∠A5=_____________________度。从上述结论中你发现了什么规律?
如图5,MA1∥NAn,则∠A1+∠A2+∠A3+……+∠An=______________________度。

180° 、360°、 540°、 720° 、 180(n-1)°。每空各2分
分析:首先过各点作MA1的平行线,由MA1∥NA2,科的各线平行,根据两直线平行,同旁内角互补,即可求得答案,注意找到规律:MA1∥NAn,则∠A1+∠A2+∠A3+…+∠An=180(n-1)度是关键.
解答:

解:如图1,
∵MA1∥NA2,
∴∠A1+∠A2=180°.
如图2,过点A2作A2C1∥A1M,
∵MA1∥NA3,
∴A2C1∥A1M∥NA3,
∴∠A1+∠A1A2C1=180°,∠C1A2A3+∠A3=180°,
∴∠A1+∠A2+∠A3=360°.
如图3,过点A2作A2C1∥A1M,过点A3作A3C2∥A1M,
∵MA1∥NA3,
∴A2C1∥A3C2∥A1M∥NA3,
∴∠A1+∠A1A2C1=180°,∠C1A2A3+∠A2A3C2=180°,∠C2A3A4+∠A4=180°,
∴∠A1+∠A2+∠A3+∠A4=540°.
如图4,过点A2作A2C1∥A1M,过点A3作A3C2∥A1M,
∵MA1∥NA3,
∴A2C1∥A3C2∥A1M∥NA3,
∴∠A1+∠A1A2C1=180°,∠C1A2A3+∠A2A3C2=180°,∠C2A3A4+∠A3A4C3=180°∠C3A4A5+∠A5=180°,
∴∠A1+∠A2+∠A3+∠A4+∠A5=720°.
从上述结论中你发现了规律:如图5,MA1∥NAn,则∠A1+∠A2+∠A3+…+∠An=180(n-1)度.
故答案为:180,360,540,720,180(n-1).

练习册系列答案
相关题目
 //
// ,
, ,
, 、
、 在
在 ,
, 平分
平分 .
.
 的度数
的度数 ,那么
,那么 :
: 的比值是否随之发生变化?若变化,找出变化规律;若不变,求出这个比值.
的比值是否随之发生变化?若变化,找出变化规律;若不变,求出这个比值. ?若存在,求出其度数;若不存在,请说明理由.
?若存在,求出其度数;若不存在,请说明理由.


 ,
, ,则∠B与∠D的关系是_____________.
,则∠B与∠D的关系是_____________.

 ,∠1=45°,则∠2=_____.
,∠1=45°,则∠2=_____.