题目内容
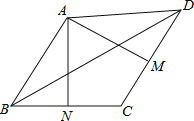
【题目】在四边形ABCD中,M、N分别是CD、BC的中点, 且AM⊥CD,AN⊥BC,已知∠MAN=74°,∠DBC=41°,则∠ADB度数为( ).
A.15°B.17°
C.16°D.32°
【答案】C
【解析】
连接AC,根据AM⊥CD,AN⊥BC,判断四边形AMCN是圆内接四边形,求出∠BCD=106°;判断∠ABD=∠ADB,根据∠ABC+∠ADC=∠ACB+∠ACD=106°,求出∠ADB即可
解:如图,连接AC,
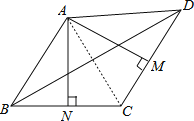 ,
,
∵AM⊥CD,AN⊥BC,
∴四边形AMCN是圆内接四边形,
∴∠MAN+∠BCD=180°,
∴∠BCD=180°-∠MAN=180°-74°=106°,
∴∠BDC=180°-41°-106°=33°,
∵M、N分别是CD、BC的中点,且AM⊥CD,AN⊥BC,
∴AB=AC=AD,
∴∠ABD=∠ADB,
∵∠ABC=∠ACB,∠ADC=∠ACD,
∴∠ABC+∠ADC=∠ACB+∠ACD=106°,
∵∠ABD=∠ADB,∠DBC=41°,∠BDC=33°,
∴∠ADB=(106°-41°-33°)÷2
=32°÷2
=16°
即∠ADB度数为16°.
故选:C

练习册系列答案
相关题目