题目内容
【题目】如图,在△ABC中,AB=AC,O为边AC上一点(不与点A,C重合),以OC为半径的圆分别交边BC,AC于点D,E,过点D作DF⊥AB于点F.
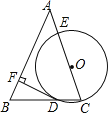
(1)求证:直线DF是⊙O的切线;
(2)若∠A=45°,OC=2,求劣弧![]() 的长.(结果保留π)
的长.(结果保留π)
【答案】(1)详见解析;(2)![]()
【解析】
(1)连结OD,根据等边对等角可得∠B=∠ACB,∠ODC=∠ACB,等量代换可得∠B=∠ODC,根据同位角相等,两直线平行可得OD∥AB,继而可得∠ODF=∠BFD=90°,由切线的判定即可求证;
(2)由两直线平行同位角相等可得:∠A=∠COD=45°,由平角性质可得:∠AOD=135°,根据弧长公式即可求解.
(1)证明:连结OD,
∵AB=AC,
∴∠B=∠ACB,
∵OC=OD,
∴∠ODC=∠ACB,
∴∠B=∠ODC,
∴OD∥AB,
∵DF⊥AB,
∴∠ODF=∠BFD=90°,
∵OD为半径,
∴直线DF是⊙O的切线;
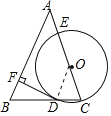
(2)解:∵∠A=45°,OD∥AB,
∴∠COD=∠A=45°
∴∠AOD=180°﹣45°=135°,
∴![]() 的长为
的长为![]() .
.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目