题目内容
【题目】如图,在平面直角坐标系中,点A,C分别在x轴,y轴上,四边形ABCO为矩形,AB=16,AC=20,点D与点A关于y轴对称,点E、F分别是线段AD、AC上的动点(点E不与点A、D重合),且∠CEF=∠ACB.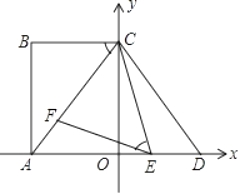
(1)直接写出BC的长是 , 点D的坐标是;
(2)证明:△AEF与△DCE相似;
(3)当△EFC为等腰三角形时,求点E的坐标.
【答案】
(1)12,(12,0)
(2)证明:∵点D与点A关于y轴对称,
∴∠CDE=∠CAO,
∵∠CEF=∠ACB,∠ACB=∠CAO,
∴∠CDE=∠CEF,
又∵∠AEC=∠AEF+∠CEF=∠CDE+∠DCE,
∴∠AEF=∠DCE,
∴△AEF∽△DCE.
(3)解:当△EFC为等腰三角形时,有以下三种情况:
①当CE=EF时,
∵△AEF∽△DCE,
∴△AEF≌△DCE,
∴AE=CD=20,
∴OE=AE-OA=20-12=8,
∴E(8,0).
②当EF=FC时,
如图所示,过点F作FM⊥CE于M,则点M为CE中点,
∴CE=2ME=![]() EF,
EF,
∵点D与点A关于y轴对称,
∴CD=AC=20,
∵△AEF∽△DCE,
∴ ![]() =
=![]() ,
,
∴AE=![]() ,
,
∴OE=AE-OA=![]() ,
,
∴E(![]() ,0).
,0).
③当CE=CF时,则有∠CFE=∠CEF,
∵∠CEF=∠ACB=∠CAO,
∴∠CFE=∠CAO,
即此时F点与A点重合,这与已知条件矛盾.
综上所述,当△EFC为等腰三角形时,点E的坐标为(8,0)或(![]() ,0).
,0).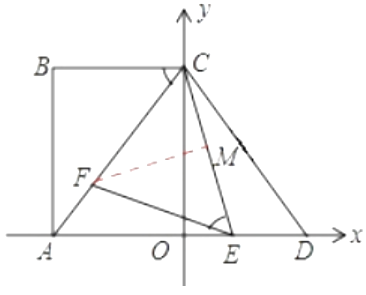
【解析】解(1)∵四边形ABCO为矩形,
∴AO=BC,AB=OC,
又∵AB=16,AC=20,
∴BC=AO=12,
∴A(-12,0),
∵点D与点A关于y轴对称,
∴D(12,0).
所以答案是:12,(12,0).
【考点精析】根据题目的已知条件,利用等腰三角形的性质和勾股定理的概念的相关知识可以得到问题的答案,需要掌握等腰三角形的两个底角相等(简称:等边对等角);直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2.