题目内容
【题目】如图,在正方形ABCD中,对角线AC与BD相交于点O,AF平分∠BAC,交BD于点F.
(1)求证: ![]() ;
;
(2)点A1、点C1分别同时从A、C两点出发,以相同的速度运动相同的时间后同时停止,如图,A1F1平分∠BA1C1 , 交BD于点F1 , 过点F1作F1E⊥A1C1 , 垂足为E,请猜想EF1 , AB与 ![]() 三者之间的数量关系,并证明你的猜想;
三者之间的数量关系,并证明你的猜想;
(3)在(2)的条件下,当A1E1=6,C1E1=4时,求BD的长
【答案】
(1)解:过F作FG⊥AB于G,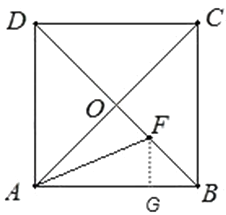
∵AF平分∠CAB,FO⊥AC,FG⊥AB,
∴OF=FG,
∵∠AOF=∠AGF=90°,AF=AF,OF=FG,
∴△AOF≌△AGF,
∴AO=AG,
直角三角形BGF中,∠DGA=45°,
∴FG=BG=OF,
∴AB=AG+BG=AO+OF= ![]() AC+OF,
AC+OF,
∴AB-OF= ![]() AC
AC
(2)解:过F1作F1G1⊥A1B,过F1作F1H1⊥BC1 , 
则四边形F1G1BH1是矩形.
同(1)可得EF1=F1G,因此四边形F1G1BH1是正方形.
∴EF1=G1F1=F1H1 ,
即:F1是三角形A1BC1的内心,
∴EF1=(A1B+BC1-A1C1)÷2…①
∵A1B+BC1=AB+A1A+BC-CC1 , 而CC1=A1A,
∴A1B+BC1=2AB,
因此①式可写成:EF1=(2AB-A1C1)÷2,
即AB-EF1= ![]() A1C1
A1C1
(3)解:由(2)得,F1是三角形A1BC1的内心,且E1、G1、H1都是切点.
∴A1E=(A1C1+A1B-BC1)÷2,
如果设CC1=A1A=x,
A1E=[A1C1+(AB+x)-(AB-x)]÷2=(10+2x)÷2=6,
∴x=1,
在直角三角形A1BC1中,根据勾股定理有A1B2+BC12=AC12 ,
即:(AB+1)2+(AB-1)2=100,
解得AB=7,
∴BD=7 ![]() .
.
【解析】(1)过F作FG⊥AB于G,根据已知条件可证△AOF≌△AGF,结合直角三角形的性质可求解;(2)过F1作F1G1⊥A1B,过F1作F1H1⊥BC1 , 根据已知条件可得四边形F1G1BH1是矩形,再证四边形F1G1BH1是正方形,则结论可证;(3)在直角三角形A1BC1中,根据勾股定理可求解。