Question

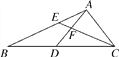
【题目】如图，在等腰直角三角形ABC中，∠BAC=90°，D，E是斜边BC上两点，∠DAE=45°，，则的面积为__________.

Answer 1

【答案】

【解析】

把△ABD绕点A逆时针旋转90°得到△ACF，连接EF，根据旋转的性质可得CF=BD，AF=AD，∠CAF=∠BAD，∠ACF=∠B=45°，然后求出∠EAF=45°，从而得到∠EAF=∠DAE，再利用“边角边”证明△AEF和△AED全等，根据全等三角形对应边相等可得EF=DE，再求出△CEF是直角三角形，利用勾股定理列式求出EF，然后求出BC，再根据等腰直角三角形的性质求出点A到BC的距离，然后利用三角形的面积公式列式计算即可得解．

解：如图，把△ABD绕点A逆时针旋转90°得到△ACF，连接EF，

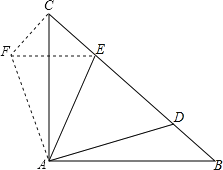
∵∠BAC=90°，AC=AB，
∴∠ACB=∠B=45°，
由旋转的性质得，CF=BD，AF=AD，∠CAF=∠BAD，∠ACF=∠B=45°，
∵∠DAE=45°，
∴∠EAF=∠CAF+∠CAE=∠BAD+∠CAE=90°-∠DAE=45°，
∴∠EAF=∠DAE，
在△AEF和△AED中，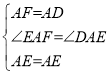
，
∴△AEF≌△AED（SAS），
∴EF=DE，
∵∠ECF=∠ACF+∠ACB=45°+45°=90°，
∴△CEF是直角三角形，
∴EF= =5，
∴BC=CE+DE+BD=4+5+3=12，

∵∠BAC=90°，AC=AB，
∴点A到BC的距离为×12=6，

∴△ABC的面积=×12×6=36．

故答案为：36.