题目内容
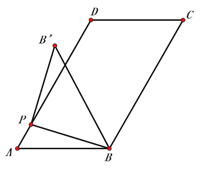
【题目】如图,平行四边形ABCD中,BD是它的一条对角线,过A、C两点作AE⊥BD,CF⊥BD,垂足分别为E、F,延长AE、CF分别交CD、AB于M、N.
(1)求证:四边形CMAN是平行四边形.
(2)已知DE=2,FN=1,求BN的长.

【答案】(1)证明见解析(2)![]()
【解析】分析:(1)、根据ABCD是平行四边形得出CD∥AB,根据垂直得出AM∥CN,从而得出平行四边形;(2)、根据平行四边形的性质得出△MDE和△NBF全等,得出BF=2,最后根据Rt△BNF的勾股定理得出BN的长度.
详解:(1)∵四边形ABCD是平行四边形, ∴CD∥AB, ∵AM⊥BD,CN⊥BD, ∴AM∥CN, ∴CM∥AN,AM∥CN, ∴四边形AMCN是平行四边形.
(2)∵四边形AMCN是平行四边形, ∴CM=AN, ∵四边形ABCD是平行四边形,
∴CD=AB,CD∥AB, ∴DM=BN,∠MDE=∠NBF, ∴△MDE≌△NBF,
∴BF=DE=2, 在Rt△BNF中,BN=![]() .
.

练习册系列答案
相关题目