Question

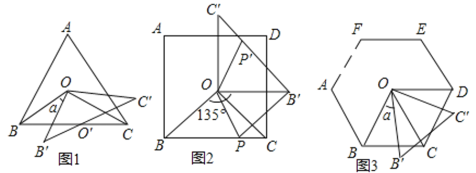
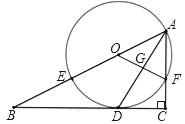
【题目】（1） 问题发现：如图， 在中，，， 点是的中点， 以点为顶点作正方形， 使点，分别在和DF上， 连接，，则线段和数量关系是 ．

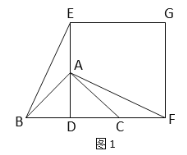
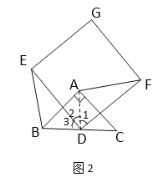
（2） 类比探究：如图， 保持固定不动， 将正方形绕点旋转，则中的结论是否成立？如果成立，请证明；如果不成立，请说明理由

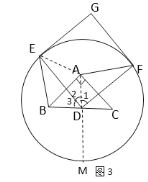
（3）解决问题：若，在的旋转过程中，连接，请直接写出的最大值

Answer 1

【答案】（1）BE＝AF；（2）成立，理由详见解析；（3）3

【解析】

(1)证明△ADF≌△BDE即可得到结论；

(2) 连接AD，证明△BDE≌△ADF即可；

(3) 由正方形DFGE绕点D旋转，故以点D为圆心DE为半径作圆，当点E旋转至点M，且点A、D、M三点共线时AE有最大值，根据等腰三角形的性质求出AD=BC=1，根据正方形的性质求出DE=DM=DF=2，即可得到AM=3.

解：（1）∵， 点是的中点，

∴AD⊥BC，BD=CD，

∴∠ADC=∠ADB=90°，

∵，，

∴∠ABC=∠ACB=45°，

∴∠BAD=∠ABC=45°，

∴AD=BD，

∵四边形为正方形，

∴DE=DF，

∴△ADF≌△BDE，

∴BE＝AF；

（2）成立，理由如下，如图2，连接AD，

∵∠BAC＝90°，AB＝AC，D为BC中点，

∴AD⊥BC，AD＝BD＝CD，

∴∠2＋∠3＝90°，

∵四边形EDFG为正方形，

∴DE＝DF，∴∠EDF＝90°，

∴∠1＋∠2＝90°，∴∠1＝∠3，

∴△BDE≌△ADF（SAS），∴BE＝AF．

（3）由正方形DFGE绕点D旋转，故以点D为圆心DE为半径作圆，当点E旋转至点M，且点A、D、M三点共线时AE有最大值，

∵∠BAC＝90°，AB＝AC，D为BC中点，

∴AD=BC=1，

∵四边形EDFG为正方形，

∴DE=DM=DF=2，

∴AM=AD+DM=1+2=3，

∴AE的最大值为3.