题目内容
【题目】如图,在矩形ABCD中,点E、F分别在边CD、BC上,且DC=3DE=3a.将矩形沿直线EF折叠,使点C恰好落在AD边上的点P处,则FP= . 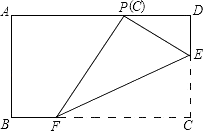
【答案】2 ![]() a
a
【解析】解:作FM⊥AD于M,如图所示:
则MF=DC=3a,
∵四边形ABCD是矩形,
∴∠C=∠D=90°.
∵DC=3DE=3a,
∴CE=2a,
由折叠的性质得:PE=CE=2a=2DE,∠EPF=∠C=90°,
∴∠DPE=30°,
∴∠MPF=180°﹣90°﹣30°=60°,
在Rt△MPF中,∵sin∠MPF= ![]() ,
,
∴FP= ![]() =
= ![]() =2
=2 ![]() a;
a;
故答案为:2 ![]() a.
a.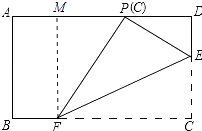
本题考查了折叠的性质、矩形的性质、三角函数等知识;熟练掌握折叠和矩形的性质,求出∠DPE=30°是解决问题的关键.作FM⊥AD于M,则MF=DC=3a,由矩形的性质得出∠C=∠D=90°.由折叠的性质得出PE=CE=2a=2DE,∠EPF=∠C=90°,求出∠DPE=30°,得出∠MPF=60°,在Rt△MPF中,由三角函数求出FP即可.

练习册系列答案
 阶梯计算系列答案
阶梯计算系列答案
相关题目







