题目内容
【题目】如图1,在平面直径坐标系中,抛物线y=ax2+bx﹣2与x轴交于点A(﹣3,0).B(1,0),与y轴交于点C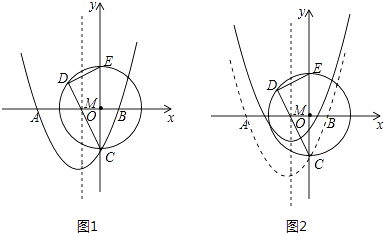
(1)直接写出抛物线的函数解析式;
(2)以OC为半径的⊙O与y轴的正半轴交于点E,若弦CD过AB的中点M,试求出DC的长;
(3)将抛物线向上平移 ![]() 个单位长度(如图2)若动点P(x,y)在平移后的抛物线上,且点P在第三象限,请求出△PDE的面积关于x的函数关系式,并写出△PDE面积的最大值.
个单位长度(如图2)若动点P(x,y)在平移后的抛物线上,且点P在第三象限,请求出△PDE的面积关于x的函数关系式,并写出△PDE面积的最大值.
【答案】
(1)
解:将点A(﹣3,0)、B(1,0)代入y=ax2+bx﹣2中,
得: ![]() ,解得:
,解得: ![]() ,
,
∴抛物线的函数解析式为y= ![]() x2+
x2+ ![]() x﹣2
x﹣2
(2)
解:令y= ![]() x2+
x2+ ![]() x﹣2中x=0,则y=﹣2,
x﹣2中x=0,则y=﹣2,
∴C(0,﹣2),
∴OC=2,CE=4.
∵A(﹣3,0),B(1,0),点M为线段AB的中点,
∴M(﹣1,0),
∴CM= ![]() =
= ![]() .
.
∵CE为⊙O的直径,
∴∠CDE=90°,
∴△COM∽△CDE,
∴ ![]() ,
,
∴DC= ![]() .
.
(3)
解:将抛物线向上平移 ![]() 个单位长度后的解析式为y=
个单位长度后的解析式为y= ![]() x2+
x2+ ![]() x﹣2+
x﹣2+ ![]() =
= ![]() x2+
x2+ ![]() x﹣
x﹣ ![]() ,
,
令y= ![]() x2+
x2+ ![]() x﹣
x﹣ ![]() 中y=0,即
中y=0,即 ![]() x2+
x2+ ![]() x﹣
x﹣ ![]() =0,
=0,
解得:x1= ![]() ,x2=
,x2= ![]() .
.
∵点P在第三象限,
∴ ![]() <x<0.
<x<0.
过点P作PP′⊥y轴于点P′,过点D作DD′⊥y轴于点D′,如图所示.

(方法一):在Rt△CDE中,CD= ![]() ,CE=4,
,CE=4,
∴DE= ![]() =
= ![]() ,sin∠DCE=
,sin∠DCE= ![]() =
= ![]() ,
,
在Rt△CDD′中,CD= ![]() ,∠CD′D=90°,
,∠CD′D=90°,
∴DD′=CDsin∠DCE= ![]() ,CD′=
,CD′= ![]() =
= ![]() ,
,
∴OD′=CD′﹣OC= ![]() ,
,
∴D(﹣ ![]() ,
, ![]() ),D′(0,
),D′(0, ![]() ).
).
∵P(x, ![]() x2+
x2+ ![]() x﹣
x﹣ ![]() ),
),
∴P′(0, ![]() x2+
x2+ ![]() x﹣
x﹣ ![]() ).
).
∴S△PDE=S△DD′E+S梯形DD′P′P﹣S△EPP′= ![]() DD′ED′+
DD′ED′+ ![]() (DD′+PP′)D′P′﹣
(DD′+PP′)D′P′﹣ ![]() PP′EP′=﹣
PP′EP′=﹣ ![]() ﹣
﹣ ![]() x+2(
x+2( ![]() <x<0),
<x<0),
∵S△PDE=﹣ ![]() ﹣
﹣ ![]() x+2=﹣
x+2=﹣ ![]() +
+ ![]() ,
, ![]() <﹣
<﹣ ![]() <0,
<0,
∴当x=﹣ ![]() 时,S△PDE取最大值,最大值为
时,S△PDE取最大值,最大值为 ![]() .
.
故:△PDE的面积关于x的函数关系式为S△PDE=﹣ ![]() ﹣
﹣ ![]() x+2(
x+2( ![]() <x<0),且△PDE面积的最大值为
<x<0),且△PDE面积的最大值为 ![]() .
.
(方法二):在Rt△CDE中,CD= ![]() ,CE=4,
,CE=4,
∴DE= ![]() =
= ![]() ,
,
∵∠CDE=∠CD′D=90°,∠DCE=∠D′CD,
∴△CDE∽△CD′D,
∴ ![]() =
= ![]() ,
,
∴DD′= ![]() ,CD′=
,CD′= ![]() ,
,
∴∴OD′=CD′﹣OC= ![]() ,
,
∴D(﹣ ![]() ,
, ![]() ),D′(0,
),D′(0, ![]() ).
).
∵P(x, ![]() x2+
x2+ ![]() x﹣
x﹣ ![]() ),
),
∴P′(0, ![]() x2+
x2+ ![]() x﹣
x﹣ ![]() ).
).
∴S△PDE=S△DD′E+S梯形DD′P′P﹣S△EPP′= ![]() DD′ED′+
DD′ED′+ ![]() (DD′+PP′)D′P′﹣
(DD′+PP′)D′P′﹣ ![]() PP′EP′=﹣
PP′EP′=﹣ ![]() ﹣
﹣ ![]() x+2(
x+2( ![]() <x<0),
<x<0),
∵S△PDE=﹣ ![]() ﹣
﹣ ![]() x+2=﹣
x+2=﹣ ![]() +
+ ![]() ,
, ![]() <﹣
<﹣ ![]() <0,
<0,
∴当x=﹣ ![]() 时,S△PDE取最大值,最大值为
时,S△PDE取最大值,最大值为 ![]() .
.
故:△PDE的面积关于x的函数关系式为S△PDE=﹣ ![]() ﹣
﹣ ![]() x+2(
x+2( ![]() <x<0),且△PDE面积的最大值为
<x<0),且△PDE面积的最大值为 ![]() .
.
【解析】(1)由点A、B的坐标利用待定系数法即可求出抛物线的解析式;(2)令抛物线解析式中x=0求出点C的坐标,根据点A、B的坐标即可求出其中点M的坐标,由此即可得出CM的长,根据圆中直径对的圆周角为90°即可得出△COM∽△CDE,根据相似三角形的性质即可得出 ![]() ,代入数据即求出DC的长度;(3)根据平移的性质求出平移后的抛物线的解析式,令其y=0,求出平移后的抛物线与x轴的交点坐标,由此即可得出点P横坐标的范围,再过点P作PP′⊥y轴于点P′,过点D作DD′⊥y轴于点D′,通过分割图形求面积法找出S△PDE关于x的函数关系式,利用配方结合而成函数的性质即可得出△PDE面积的最大值.
,代入数据即求出DC的长度;(3)根据平移的性质求出平移后的抛物线的解析式,令其y=0,求出平移后的抛物线与x轴的交点坐标,由此即可得出点P横坐标的范围,再过点P作PP′⊥y轴于点P′,过点D作DD′⊥y轴于点D′,通过分割图形求面积法找出S△PDE关于x的函数关系式,利用配方结合而成函数的性质即可得出△PDE面积的最大值.
【考点精析】利用二次函数的性质对题目进行判断即可得到答案,需要熟知增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小.

 全程金卷系列答案
全程金卷系列答案 快乐5加2金卷系列答案
快乐5加2金卷系列答案