题目内容
【题目】如图，△ABC的三边AB、BC、CA的长分别为40、50、60，其三条角平分线交于点O，则S△ABO：S△BCO：S△CAO等于 ( )
A. 1:2:3 B. 2:3:4 C. 3:4:5 D. 4:5:6
【答案】D
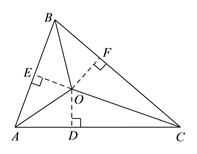
【解析】如图，过点O作OD⊥AC于点D，作OE⊥AB于点E，作OF⊥BC于点F，
∵AO、BO、CO分别平分△ABC的三个内角，
∴OD=OE=OF，
又∵S△ABO=
AB·OE，S△BCO=
BC·OF，S△ACO=
AC·OD，
∴S△ABO：S△BCO：S△CAO=
AB·OE： 
BC·OF： 
AC·OD=AB：BC：AC，
又∵AB=40，BC=50，AC=60，
∴S△ABO：S△BCO：S△CAO=40:50:60=4:5:6.
故选D.
练习册系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目
