Question

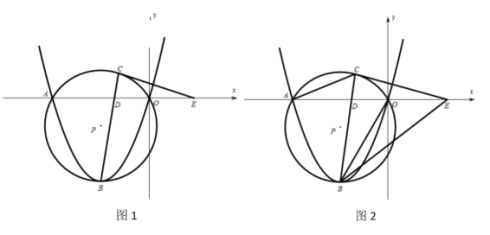
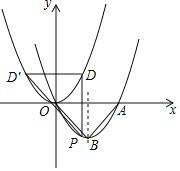
【题目】如图，在平面直角坐标系中有抛物线y＝a（x﹣2）2﹣2和y＝a（x﹣h）2，抛物线y＝a（x﹣2）2﹣2经过原点，与x轴正半轴交于点A，与其对称轴交于点B；点P是抛物线y＝a（x﹣2）2﹣2上一动点，且点P在x轴下方，过点P作x轴的垂线交抛物线y＝a（x﹣h）2于点D，过点D作PD的垂线交抛物线y＝a（x﹣h）2于点D′（不与点D重合），连接PD′，设点P的横坐标为m：

（1）①直接写出a的值；

②直接写出抛物线y＝a（x﹣2）2﹣2的函数表达式的一般式；

（2）当抛物线y＝a（x﹣h）2经过原点时，设△PDD′与△OAB重叠部分图形周长为L：

①求的值；

②直接写出L与m之间的函数关系式；

（3）当h为何值时，存在点P，使以点O、A、D、D′为顶点的四边形是菱形？直接写出h的值．

Answer 1

【答案】（1）①；②y＝﹣2x；

（2）①1；

②L＝；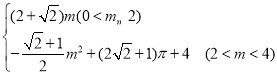

（3）h＝±．

【解析】

（1）①将x＝0，y＝0代入y＝a（x﹣2）2﹣2中计算即可；②y＝﹣2x；

（2）将（0，0）代入y＝a（x﹣h）2中，可求得a＝，y＝x2，待定系数法求OB、AB的解析式，由点P的横坐标为m，即可表示出相应线段求解；

（3）以点O、A、D、D′为顶点的四边形是菱形，DD′＝OA，可知点D的纵坐标为2，再由AD＝OA＝4即可求出h的值．

解：（1）①将x＝0，y＝0代入y＝a（x﹣2）2﹣2中，

得：0＝a（0﹣2）2﹣2，

解得：a＝；

②y＝﹣2x；．

（2）∵抛物线y＝a（x﹣h）2经过原点，a＝；

∴y＝x2，

∴A（4，0），B（2，﹣2），

易得：直线OB解析式为：y＝﹣x，直线AB解析式为：y＝x﹣4

如图1，

，

①

②如图1，当0＜m≤2时，L＝OE+EF+OF＝，

当2＜m＜4时，如图2，设PD′交x轴于G，交AB于H，PD交x轴于E，交AB于F，

则，

，

∵DD′∥EG

，即：EGPD＝PEDD′，得：EG（2m）＝（2m﹣m2）2m

∴EG＝2m﹣m2，EF＝4﹣m

∴L＝EG+EF+FH+GH＝EG+EF+PG

；

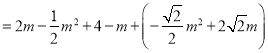
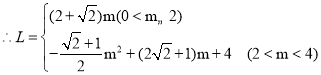（3）如图3，

∵OADD′为菱形

∴AD＝AO＝DD′＝4，

∴PD＝2，