题目内容
【题目】已知二次函数y=ax2+bx﹣3(a≠0),且a+b=3.
(1)若其图象经过点(﹣3,0),求此二次函数的表达式.
(2)若(m,n)为(1)中二次函数图象在第三象限内的点,请分别求m,n的取值范围.
(3)点P(x1,y1),Q(x2,y2)是函数图象上两个点,满足x1+x2=2且x1<x2,试比较y1和y2的大小关系.
【答案】(1)y=x2+2x﹣3;(2)﹣3<m<0;(3)y2﹣y1=(x2﹣x1)(a+3),①当a>﹣3时,y2>y1,②当a=﹣3时,y2=y1,③当a<﹣3时,y2<y1.
【解析】
(1)将点的坐标代入函数,可得a、b,即得到二次函数的表达式.(2)根据抛物线的图象,可得m,n的取值范围.(3)根据二次函数表达式,可得y2﹣y1=(x2﹣x1)(a+3),分析a的取值范围,可得到y1和y2的大小关系.
解:(1)由题意得:![]() ,
,
解得:![]() ,
,
∴此二次函数的表达式为:y=x2+2x﹣3;
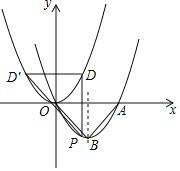
(2)如图,∵y=x2+2x﹣3=(x+1)2﹣4,且(m,n)是二次函数图象在第三象限内的点,
∴﹣4≤n<0,
当y=0时,x2+2x﹣3=0,
x=﹣3或1,
∴图象过(1,0)和(﹣3,0),
∴﹣3<m<0;
(3)由条件可得:y1=ax12+(3﹣a)x1﹣3,y2=ax22+(3﹣a)x2﹣3,
∴y2﹣y1=(x2﹣x1)[a(x2+x1)+3﹣a],
∵x1+x2=2且x1<x2,
∴y2﹣y1=(x2﹣x1)(a+3),
①当a>﹣3时,y2>y1,
②当a=﹣3时,y2=y1,
③当a<﹣3时,y2<y1.

【题目】某商场进行促销活动,出售一种优惠购物卡(注:此卡只作为购物优惠凭证不能顶替货款),花300元买这种卡后,凭卡可在这家商场按标价的8折购物.若不够卡购物和使用优惠卡购物分别视为方式一购物和方式二购物,且设顾客购买商品的金额为![]() 元.
元.
(Ⅰ)根据题意,填写下表:
商品金额(元) | 300 | 600 | 1000 | … |
|
方式一的总费用(元) | 300 | 600 | 1000 | … | |
方式二的总费用(元) | 540 | … |
(Ⅱ)顾客购买多少元金额的商品时,买卡与不买卡花钱相等?
(Ⅲ)小张要买一台标价为3500元的冰箱,如何购买合算?小张能节省多少元钱?
(Ⅳ)小张按合算的方案,把这台冰箱买下,如果该商场还能盈利![]() ,那么这台冰箱的进价是多少元?
,那么这台冰箱的进价是多少元?