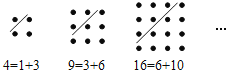题目内容
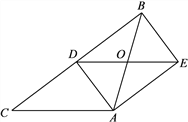
【题目】如图,某点从数轴上的A点出发,第1次向右移动1个单位长度至B点,第2次从B点向左移动2个单位长度至C点,第3次从C点向右移动3个单位长度至D点,第4次从D点向左移动4个单位长度至E点,…,依此类推,经过_________次移动后该点到原点的距离为2019个单位长度.
![]()
【答案】4037或4038
【解析】
根据数轴上点的坐标变化和平移规律(左减右加),分别求出点所对应的数,进而求出点到原点的距离;然后对奇数项、偶数项分别探究,找出其中的规律(相邻两数都相差3),写出表达式就可解决问题.
解:由图可得:第1次点A向右移动1个单位长度至点B,则B表示的数为0+1=1;
第2次从点B向左移动2个单位长度至点C,则C表示的数为1-2=-1;
第3次从点C向右移动3个单位长度至点D,则D表示的数为-1+3=2;
第4次从点D向左移动4个单位长度至点E,则点E表示的数为2-4=-2;
第5次从点E向右移动5个单位长度至点F,则F表示的数为-2+5=3;
…;
由以上数据可知,当移动次数为奇数时,点在数轴上所表示的数满足:![]() (n+1),
(n+1),
当移动次数为偶数时,点在数轴上所表示的数满足:-![]() n,
n,
当移动次数为奇数时,若![]() (n+1)=2019,则n=4037,
(n+1)=2019,则n=4037,
当移动次数为偶数时,若-![]() n=-2019,则n=4038.
n=-2019,则n=4038.
故答案为:4037或4038.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
【题目】将图1中的正方形剪开得到图2,则图2中共有4个正方形;将图2中的一个正方形剪开得到图3,图3中共有7个正方形;将图3中4个较小的正方中的一个剪开得到图4,则图4中共有10个正方形,照这个规律剪下去……

(1)根据图中的规律补全下表:
图形标号 | 1 | 2 | 3 | 4 | 5 | 6 |
| n |
正方形个数 | 1 | 4 | 7 | 10 |
|
(2)求第几幅图形中有2020个正方形?